Parabolă și ecuația canonică

În cele din urmă! Ea este cel mai mult. Gata să dezvăluie multe secrete. Ecuația canonică are forma unei parabole. în cazul în care - numărul real. Este ușor de observat că, în parabole poziție normală „situată pe o parte“, iar vârful său se află la originea. Funcția setează ramura superioară a liniei, iar funcția - ramura inferioară. Evident, parabola este simetrică în jurul unei axe. De fapt, ceea ce a crescut:

Decizie. vârful este cunoscut, se va găsi puncte suplimentare. Ecuația definește arcul superior al unei ecuații parabole - arc inferior.

Pentru a reduce calculul de înregistrare va petrece „sub un pieptene“:

Pentru o înregistrare compact, rezultatele pot fi intabulate.

Înainte de a efectua un simplu desen pointwise, formularea strictă

O parabolă este mulțimea tuturor punctelor în plan echidistant față de un punct dat și o anumită linie. nu trece prin.

Punctul este numit punctul focal al parabolei, drept - directoare (scris cu un „es“) parabole. Constant „PE“, ecuația canonică se numește parametru focal. care este egală cu distanța de la focalizarea la directricea. În acest caz. Astfel, focalizarea are coordonate. și directoarei dată de ecuația.
În exemplul nostru:

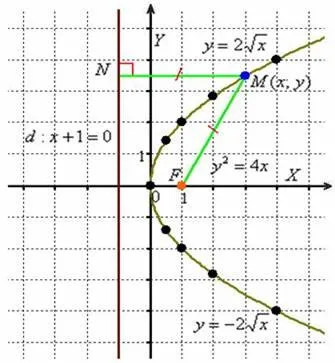
Definiția înțeles chiar Parabola mai simplă decât determinarea elipsei și hiperbola. Pentru orice punct al parabolei lungimii segmentului (distanța de la focar la un punct) este egal cu lungimea perpendicularei (distanța de la punctul de la directricea):

Felicitări! Mulți dintre voi ați făcut astăzi este adevărata descoperire. Se pare, hiperbole si parabole nu sunt la toate funcțiile de diagrame „obișnuite“, și au o origine geometrică pronunțată.

Evident, nu va fi „auzit“ în sus și în jos, se apropie de infinit aproape de axa cu creșterea parametrului focal ramură generat. Atunci când reducerea aceleași valori „pe“ ei încep să comprime și să se extindă de-a lungul axei

Excentricitatea fiecărui parabole este egală cu una din urmatoarele: