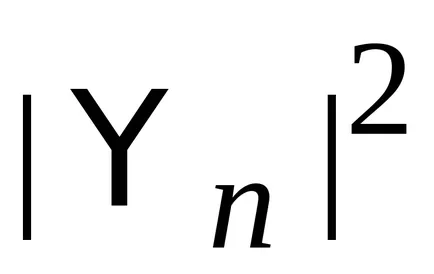operatorii hermitian
Cantitatea reală fizică, dimensiunea sa - cu siguranță. Aceste condiții pentru valorile proprii ale unui operator Hermitian oferă. Operațiunea Hermitian conjugare este determinată de forma pătratică integrală. Această formă descrie, printre altele, valoarea medie a măsurandului.
adjoint hermitian
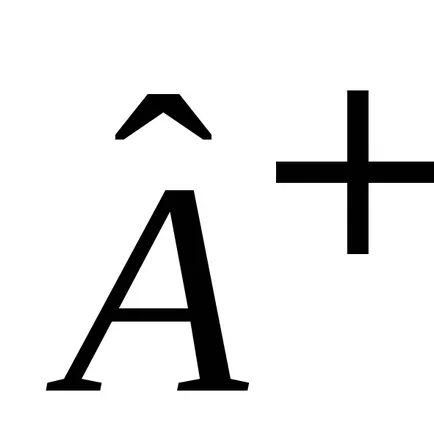
Integrarea se realizează pe parcursul întregului volum al spațiului în care poate exista o particulă.
Proprietăți de conjugare Hermitian
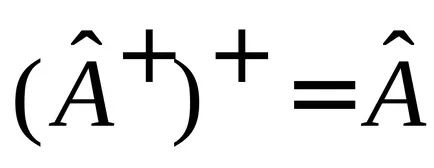
,
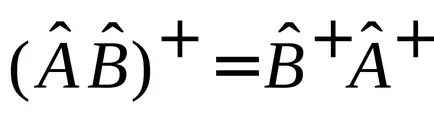
pentru a dovedi
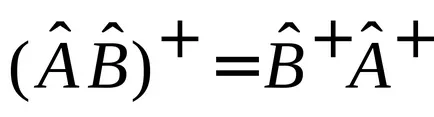
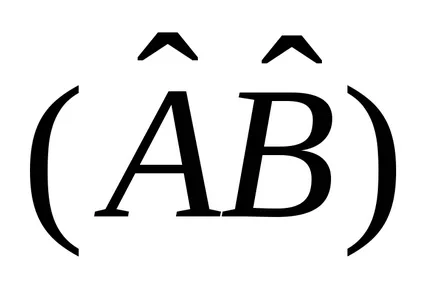
și secvențial - mai întâi operatorului

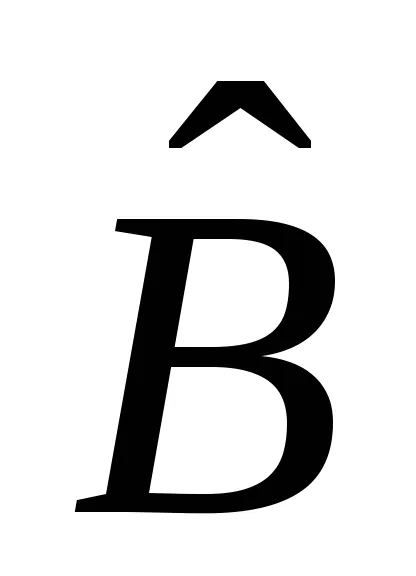
.
Comparați partea dreaptă a ecuațiilor obținute.
Relațiile rămase se dovedesc.
Operatorul Hermitian nu se schimbă atunci când conjugării Hermitian
Din (2.11) obținem definiția unui operator Hermitian
Prin urmare, operatorul Hermitian poate fi mutat într-o formă pătratică integral de la o funcție la alta.
Proprietățile operatorului Hermitian.
1) Valorile proprii sunt reale.
cred în cazul în care
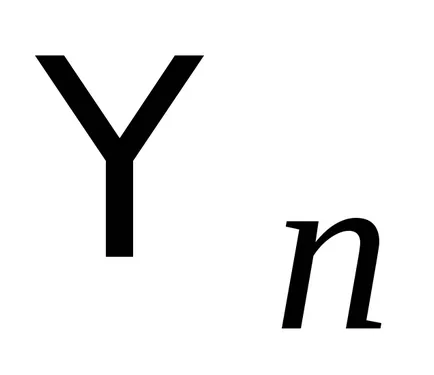

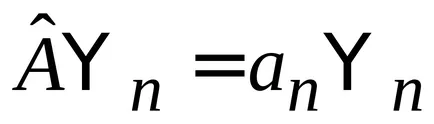
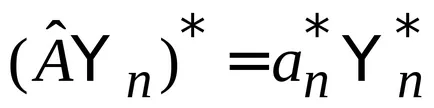
.
- valoarea măsurată este real.
2) funcțiile proprii corespunzătoare diferitelor valori proprii sunt ortogonale.
Pentru propriile lor funcții
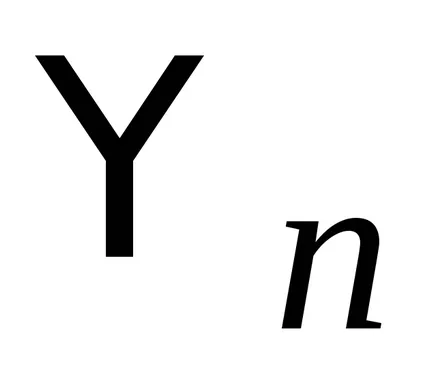
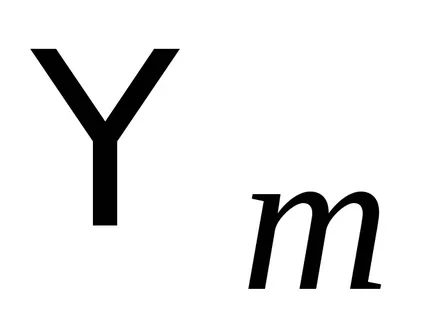

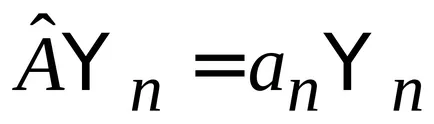
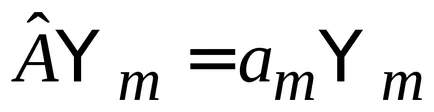
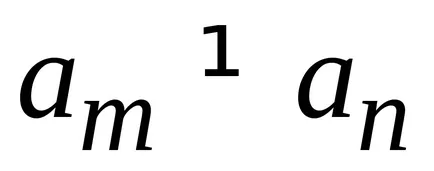
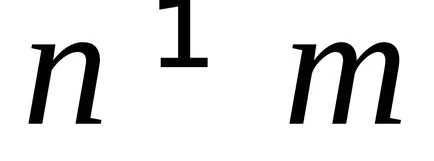
.
Având în vedere valorile proprii sunt reale (2.15), vom găsi
.
la
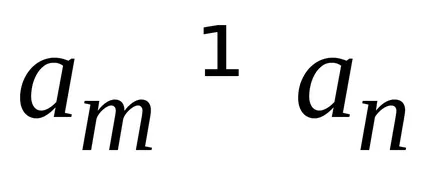
În consecință, statul
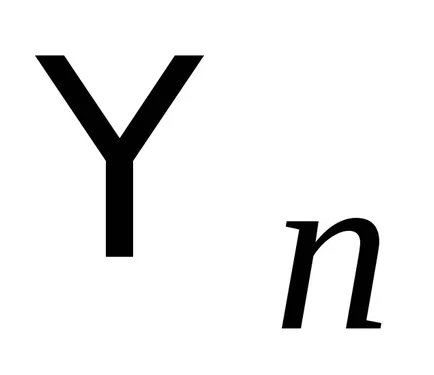
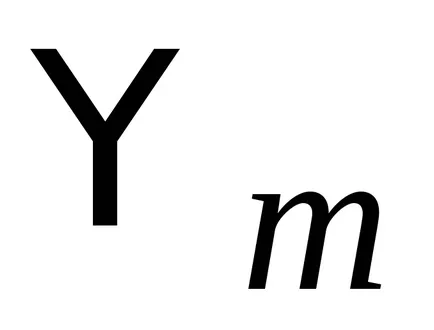
operator de impuls Hermitian
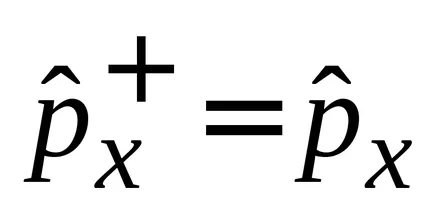
partea stângă a operatorului
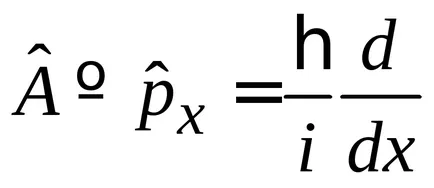
.
Partea din dreapta (2.14)
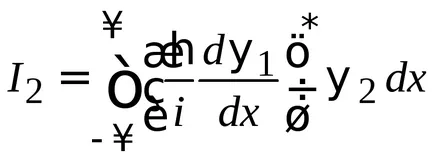
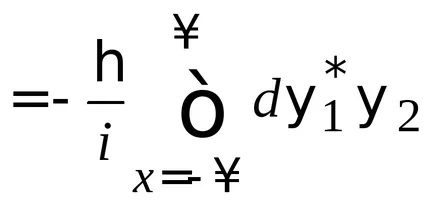
.
Funcțiile de undă pătrat integrabile și dispar la infinit, așa
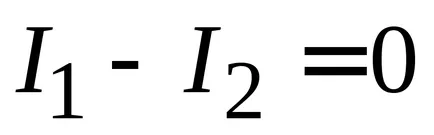
Termeni ortonormalitate
Setul de funcții proprii oricărui operator Hermitian

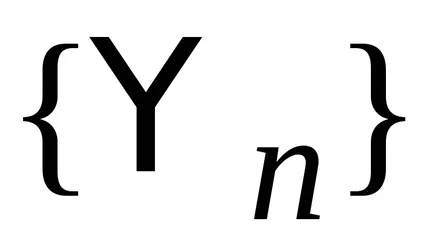

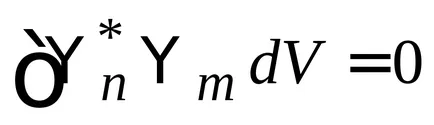
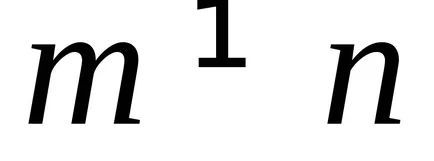
spektrn discret. normalizare
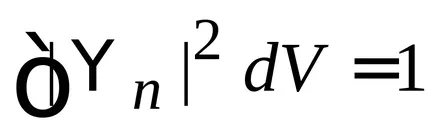
unde
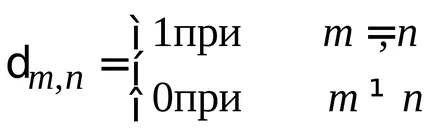
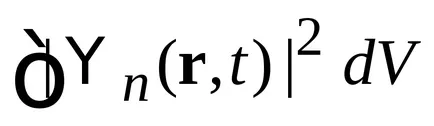
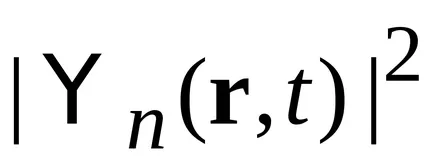
spektrn continuă. În cazul în care indicele este o funcție privată ia valori continue, atunci (2.21) în locul simbolului este pus funcția delta Kronecker
la