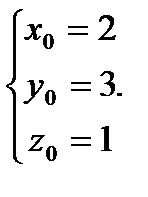o ecuație linie dreaptă în spațiu - studopediya
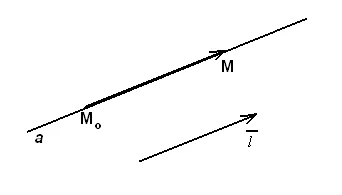
În spațiul direct o. trecând prin punctul paralel cu vectorul. numitul ghid și vector direct (Figura 14).
Să punctul - punctul de curent continuu. Vector se află pe calea cea dreaptă coliniar cu. Din condiția de coliniaritate a doi vectori, avem:
Aceste ecuații - ecuațiile canonice ale unei linii drepte în spațiu.
Dacă ecuațiile canonice pentru a introduce un parametru t:. Obținem ecuațiile parametrice ale liniei:
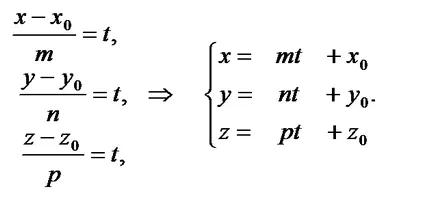
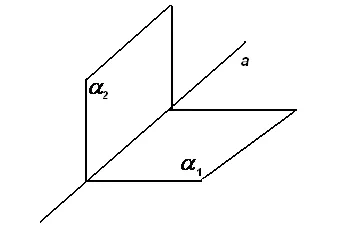
Linia poate fi definită ca intersecția a două plane (Figura 15):
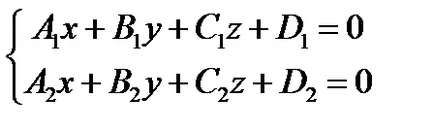
o ecuație linie dreaptă care trece prin cele două puncte și.
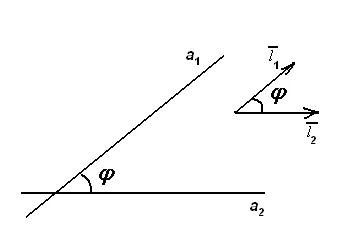
Unghiul dintre liniile este egal cu unghiul ascuțit dintre vectorii lor de direcție (fig.16) și se calculează cu formula:
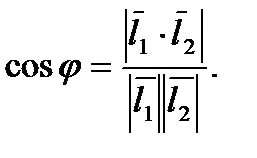
Exemplu. set de ecuații generale directe
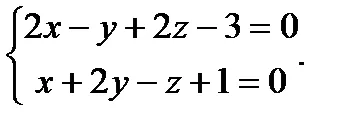
a) Scrie această linie pentru ecuațiile canonice și parametrice;
b) Găsiți unghiul dintre linia dreaptă și linia dreaptă dată de ecuațiile
a) Alegeți unul din punctele prin care trece respectiva linie definită de intersecția de avioane. Sistemul inițial are un număr infinit de soluții, dintre care unul a primit una dintre variabilele care dau o anumită valoare. Să. apoi valorile celorlalte necunoscutelor se găsesc din sistem
Soluția acestui sistem este o pereche de numere.
Ca rezultat, vom obține punctul. prin care linia dorită. Ca un ghid vă poate lua un vector direct. în cazul în care. - vectorii normali de avioane care trec linia care este o linie dreaptă. Astfel,
Să ne scrie ecuațiile canonice ale unei linii drepte.
Se obțin din ecuațiile parametrice canonice ale liniei drepte:
b) vectorul de direcție al liniei. vector direcția unui unghi drept între linii și este egal cu unghiul ascuțit dintre vectorii lor direcție:
Unghiul dintre linia dreaptă și planul
Să presupunem că avem o linie dreaptă și plan (Figura 17):
c Direct vector direcție
Avionul cu vectorul normal de
Unghiul dintre linia dreaptă și un plan se calculează cu formula:
Pentru a găsi punctul de intersecție al liniei și planul. Trebuie să direcționeze ecuațiile parametrice
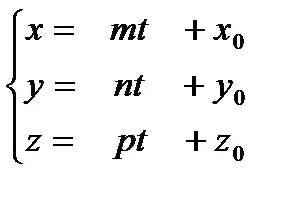
Exemplu. Găsiți a) unghiul dintre linia dreaptă și planul;
b) punctul de intersecție al liniei și planul.
.
Decizie. - normală la planul; - vectorul direcția liniei.
b) înlocuirea ecuațiile parametrice ale liniei drepte
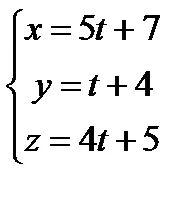
. - stabilirea punctului de intersecție al liniei și planul.
Înlocuim valoarea parametrului în ecuațiile parametrice, obținem: