Momentul de inerție al secțiunilor plane
momentul secțiunii de inerție axial (al doilea moment al zonei sau al doilea moment de inerție) în jurul axei x este suma produselor ariilor elementare dA cu pătratul distanțele lor față de axa care este numeric egală cu integrala
$$ J_x = \ int_y ^ 2DA $$
Și în ceea ce privește axa y:
$$ J_y = \ int_x ^ 2DA $$
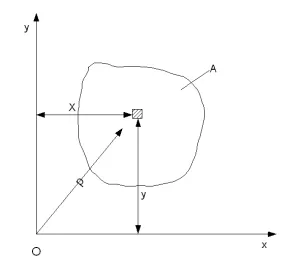
unde y - distanța de la zona elementară dA la x (a se vedea figura) a arborelui,
x - distanța de la zona dA elementar pe axa y.
Polar momentul de inerție în raport cu un anumit punct
(Poli Chemat) este suma produselor din zonele elementare dA cu pătratul distanței lor de la acest punct:
$$ J_ = \ int_ ^ 2DA $$
unde [math] \ rho [/ math] - dA departe de site-ul la polul despre care se calculează momentul de inerție polar.
centrifugal momentul de inerție față de axele x și y este suma lucrărilor de pe suprafețele elementare dA ale distanței dintre aceste axe:
$$ J_ = \ int_x y dA $$
unde x, y - distanța de la zona elementară dA la axele x și y (a se vedea figura).
Inerția centrifugă poate fi pozitiv, negativ, iar în cazul special de la zero. Atunci când axele perpendiculare între x și y sau una dintre ele sunt axe de simetrie a figurii, axele relative de inerție centrifugal este zero. [Math] J_ = 0 [/ math].
Polar momentul de inerție unii - orice punct este egal cu suma momentelor de inerție axial aproximativ două axe perpendiculare între ele care trec prin acest punct. $$ J_ = J_x + J_y $$
Relația dintre momentele de inerție în jurul axelor paralele
Formule pentru momentele de inerție axelor de transfer paralel:
$$ J_> = \ int_ (y + a) ^ 2DA = J_ + 2aS_x + o ^ 2A $$
$$ J_> = \ int_ (x + b) ^ 2DA = J_ + 2bS_y + b ^ 2A $$
$$ J_y_1> = \ int_ (y + a) (x + b) dA = J_ + aS_y + bS_x + aba $$
Momentul de inerție în jurul oricărei axe egală cu momentul de inerție
în raport cu axa centrală paralelă cu aceasta, plus produsul dintre piesele pătrate pe distanța pătratică între axe.
Momentul de inerție în jurul axei centrale se numește punctul central de inerție.
Din formulele, rezultă că momentul de inerție față de axa centrală mai mică decât momentul de inerție în jurul oricărei axe paralele cu secțiunea excentrică centru.
Relația dintre momentele de inerție la rotirea osii
$$ J_ = J_x cos ^ 2 \ alpha + J_y păcat ^ 2 \ alfa - J_ sin (2 \ alpha) $$
$$ J_ = J_x păcat ^ 2 \ alpha + J_y cos ^ \ alpha + J_ sin (2 \ alfa) 2 $$
și momentul de inerție centrifug: $$ J_ = * sin (2 \ alfa) + J_ cos (2 \ alpha) $$
Unele proprietăți sectioante momente de inerție
- Dimensiunea - lungime 4 (în general 4 cm)
- momentelor axiale și polare de inerție - valori sunt întotdeauna pozitive, deoarece un coordonate de site arbitrare sunt incluse în formula în pătrat.
- Atunci când cotitură cantitatea de osii momentelor de inerție axial nu este schimbat. $$ J_ + J_ = J_x + J_y $$
- Polar momentul de inerție în jurul punctului axial este suma momentelor de inerție două axe perpendiculare între ele care trec prin acest punct: [matematica] J_p = J_x + J_y [/ math]
- Momentul de inerție al secțiunii compozit este suma momentelor de inerție ale elementelor secțiunii.