Mișcarea circumferențial
Mișcarea de-a lungul circumferinței. Ecuația de mișcare de-a lungul circumferinței. Viteza unghiulară.
Medie = accelerația centripetă. Perioada, frecvența de revoluție (rotație).
liniar Comunicare și viteza unghiulară.
Mișcarea de-a lungul circumferinței.
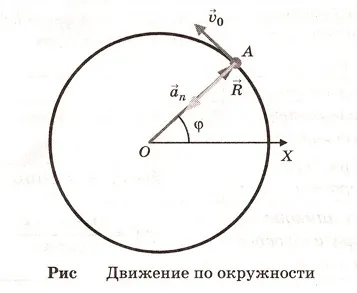
Poziția punctului A. circumferențial se deplasează cu viteză constantă v în modul în orice moment t este determinată de unghiul φ dintre axa și raza OX-vetorom:
Ecuația de mișcare de-a lungul circumferinței. Viteza unghiulară. Medie = accelerația centripetă. Perioada, frecvența de revoluție (rotație). Relația dintre viteza unghiulară lineară și:
Viteza unghiulară [ω] = 1 rad / s = 1 s -1 este: relație δφ de deplasare unghiulară în intervalul de timp pentru această perioadă AT:
Ecuația cinematic de mișcare a corpului cu o modulo viteză constantă pe circumferință.
-
- unde: φ - unghiul, ω - viteza unghiulară
Normal (centripetă) accelerare: caracterizează viteza de schimbare a vectorului de viteză liniară. Vectorul este întotdeauna îndreptat spre centrul cercului se exprimă după cum urmează:
Perioada (rotire) [T] = 1 este: Timpul unei rotații. În cazul în care cererile punctul sovershaetN pentru timpul t. atunci:
Tratament Rate (rotire) [n] = 1 / c = 1 s -1 este: Câte de rotații pe unitatea de timp este făcută = cantitate egală cu numărul de rotații pe secundă:
liniar de comunicare și viteza unghiulară între ele și cu perioada de circulație: