mișcare uniformă și neuniformă a corpului de-a lungul circumferinței

Un caz special de mișcare curbilinie - o mișcare circulară. mișcare circulară, chiar și uniformă, există întotdeauna o mișcare accelerată: viteza modulului tot timpul îndreptate la o tangentă la traiectoria, în continuă schimbare de direcție, astfel încât vectorul accelerație la o mișcare circulară spre centrul cercului și perpendicular pe vectorul viteză.

Circumferința - formă plată, astfel încât mișcarea în mișcarea circumferențială este plană.

mișcare circulară uniformă - o mișcare în care organismul pentru intervale de timp regulate descrie același arc.

poziția corpului pe cercul definit de către vectorul raza $ \ overrightarrow = R $, trase din centrul cercului. raza egală cu raza cercului unitate de vectorul: $ \ left | \ overrightarrow \ dreapta | = R $.

Figura 1. Viteza de mișcare și de deplasare de-a lungul circumferinței

In timpul corpului At, trecerea de la punctul A la punctul B, face ca mutarea $ \ r $ triunghi, egală cu coarda AB, și trece calea egală cu lungimea arcului l. Vectorul Raza se rotește $$$$. Unghiul exprimat în radiani.

Rata de $ \ $ overrightarrow mișcare organism într-un cerc tangent la traiectoria. Se numește viteza liniară. viteză liniară Modul egală cu raportul dintre lungime l la lungimea arcului de timp $ \ triunghi t $, pentru care este trecut arc: $ v = \ frac $

mărime fizică scalară este numeric egal cu unghiul de rotație raportul vectorului razei la perioada de timp în care are loc această schimbare, numită viteza medie unghiulară: $ \ omega = \ frac $. Unitatea SI a vitezei unghiulare este radiani pe secundă.

În mișcare uniformă circumferențial unghiulară a vitezei și a vitezei liniare Modul --- valoare constanta: $ = $ const; $ V = const $.

Poziția corpului poate fi determinată dacă modulul cunoscut vector rază $ \ overrightarrow $ și $$ unghiul pe care îl face cu axa Ox $ $ (axa unghiulară). Dacă inițial timp $ t_0 = 0 $ este unghiular de coordonate $ \ varphi $ 0, iar la momentul t este egal cu $ \ varphi $, atunci unghiul de rotație $ Δ $$ \ varphi $ vector rază în timpul $ = t At -t_0 $ este egal cu $ Δ $$ \ varphi $ = $ \ varphi $$ \ varphi $ 0 ° C. Apoi, ultima formula se poate obține legea de mișcare uniformă a unui punct de pe un cerc:

$ \ Varphi = \ varphi_0 + \ omega T $

Acesta vă permite să se determine poziția corpului în orice moment $ t $.

Având în vedere că $ \ triunghi \ varphi = \ frac $, obținem formula conexiune între viteza unghiulară lineară și: $ \ omega = \ frac = \ frac $

Atunci când se deplasează într-un cerc, ca în orice mișcare curbilinie, accelerația poate fi exprimată ca suma normală $ _n $ și $ _ $ componente tangențiale: $ \ overrightarrow = _ + _ n $

Cu o viteză circulară uniformă mișcare liniară este constantă, iar componenta tangențială a accelerației _ $> = $ 0 ° C. Prin urmare, în acest caz, $ \ overrightarrow = _n $.

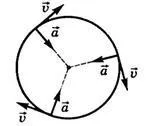
Figura 2. Accelerația și viteza de mișcare la circumferențiale uniformă

Accelerația mișcarea circulară uniformă

În plus accelerare centripete, mișcare uniformă a celor mai importante caracteristici sunt circumferential perioada și frecvența tratamentului.

Circulatie Perioada de $ T = \ frac = \ frac $ - acesta este momentul în care organismul face o revoluție.

rata de conversie $ \ \ \ = Nu \ frac $ --- este o valoare care este numeric egal cu numărul de rotații efectuate pe unitatea de timp. Frecventa masurata 1 / s.

Perioada și frecvența - valoarea reciprocă: $ \ Nu = \ frac $

La o frecvență constantă a revoluției accelerației centripete este direct proporțională cu distanța de particula se deplasează la centrul de rotație.

mișcare circulară inegala este diferită de uniforma numai prin aceea că componenta tangențială a accelerației $ _> \ ne 0 $, iar viteza v liniar (t) și viteza unghiulară $$ (t) sunt instabile și sunt funcții de timp.

În cazul mișcării uniform accelerate de-a lungul unui cerc

Coordonatele unghiulare pentru deplasarea de-a lungul unui cerc cu o angulară viteză $ \ omega \ stânga (t \ dreapta) Frac = \ $, iar accelerația unghiulară $ \ varepsilon = \ frac = \ frac $, să obțină drept uniform accelerat de mișcare de-a lungul circumferinței: $ \ varphi \ stânga (t \ dreapta) = _ 0+ \ omega \ stânga (t \ dreapta) t + \ varepsilon \ frac $. în cazul în care $ \ omega \ stânga (t \ dreapta) = \ frac ;; \ \ \ \ \ varepsilon = \ frac> $.