metode iterative

Cu un număr mare de necunoscute ale sistemului liniar de ecuații scheme de eliminare Gauss, care dă o soluție exactă, devine destul de dificil. În acest caz, pentru a găsi rădăcinile mai ușor de utilizat metode iterative aproximative. Să considerăm metoda iterația (metoda Seidel).

Având în vedere un sistem

Presupunând că termenii diagonală - coeficienții sunt non-zero,

(I = 1, ..., n), rezolva sistemul de ecuații în raport cu primul

, al doilea - în ceea ce privește

etc. Apoi obținem un sistem echivalent:

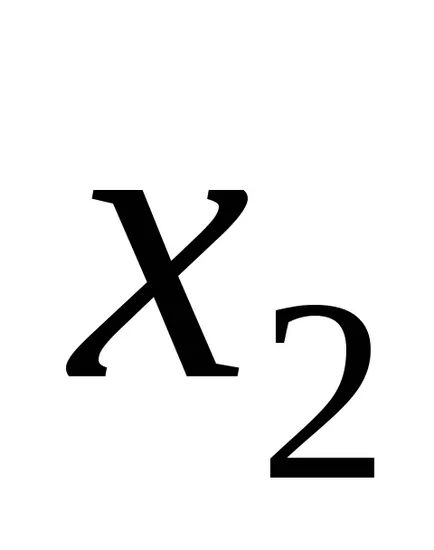
Sistemul (2) se realizează prin aproximări succesive. Ca apropierea de zero poate lua orice valoare. folosesc adesea acest lucru ca pe o coloană de termeni liberi.

Aproximarea următoare se calculează prin substituirea valorilor

în partea dreaptă a ecuațiile (2). In forma de matrice, primă aproximație este exprimată ca:

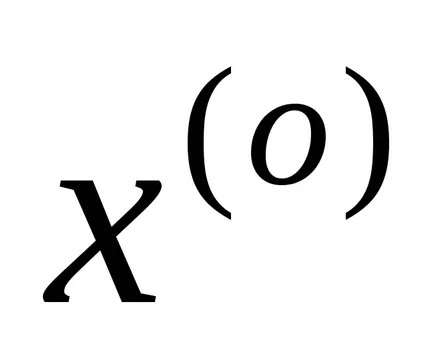
a doua aproximare se calculează prin primul:

În cazul în care secvența de aproximări

Ea are o limită

această limită este o soluție de (2) și, în consecință, sistemul (1).

Scriem formula aproximări în formă extinsă:

Metoda aproximațiilor succesive, definită prin formula (3) se numește prin iterație. Procesul iterativ converge bine, adică aproximări numerice necesare pentru obținerea sistemului radicular (1) cu o anumită precizie este mică, în cazul în care elementele matricei

mici în magnitudine. Ie pentru aplicarea cu succes a procesului de iterare elementelor diagonale ale modulelor sistemului (1) trebuie să fie mare în comparație cu coeficienții non-diagonale ale modulelor sistemului. Valorile membrilor liberi ai sistemului (1) cu privire la rezultatul deciziei nu este afectată.

Luați în considerare sistemul de ecuații algebrice liniare cu trei necunoscute:

Selectăm partea dreaptă a fiecărei necunoscute diagonală ecuație

(Inițial) se apropie de zero până la rezolvarea unora dintre valorile pe care le alege necunoscut și le lăsați

. Substituind aproximarea inițială a sistemului (2)

Sistemul (3) pentru a calcula necunoscut

și

utilizate numai că valorile calculate ale necunoscutele din iterația curentă.

În general, la acel sistem K- iterație se pare ca acest lucru:

Aceasta este, valoarea curentă a necunoscut utilizat imediat pentru calculele ulterioare. Această metodă se numește metoda iterativă de Gauss - Seidel.

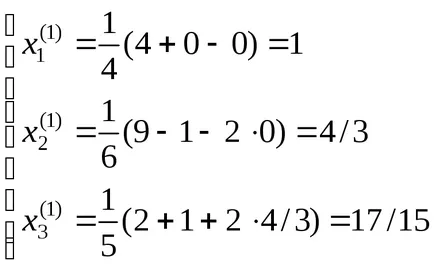
soluția exactă cerută de procesul iterativ () vor fi primite în iterația 5-6-lea.

În cazul unui sistem de n ecua k - th aproximare a soluției ar fi:

Procesul iterativ continuă până când toate

nu se va închide

. criteriu de proximitate poate fi o condiție

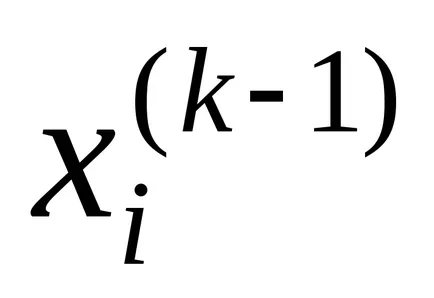
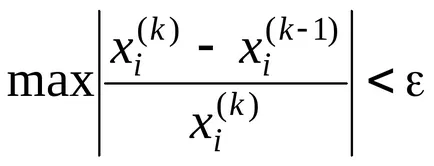
Luați în considerare metoda de aspecte legate de convergența. Având în vedere un sistem de două ecuații

De la (1) și (3) obținem

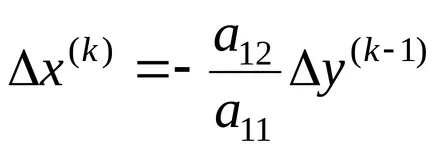
Din ultima ecuație urmează:

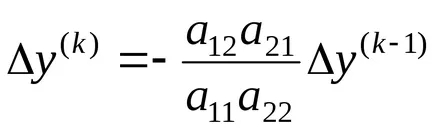
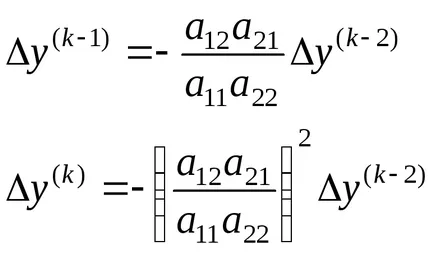
Continuând, puteți obține:

Rezultă că procesul iterativ de Gauss - Seidel

converge dacă abordarea iterație K- va fi semnificativ diferită de prima aproximare. Acest lucru este posibil numai cu condiția:

ceea ce înseamnă că membrii diagonale prevalează asupra celorlalte.

Avantajul metodei de eliminare este că este finit și, teoretic, poate fi folosit pentru a rezolva orice sistem nedegenerata de ecuații algebrice liniare. Iterativa Metoda Gauss-Seidel converge numai pentru sistemele speciale de ecuații. Cu toate acestea, în cazul în care metoda iterativ converge, este de preferat să:

timpul de calcul

o iterație, în timp ce pentru a evita timpul este metoda proporțională

, în cazul în care decizia este primită cu mai puțin de iterații Zan, metoda iterativă pentru costurile totale vor fi mai mici.

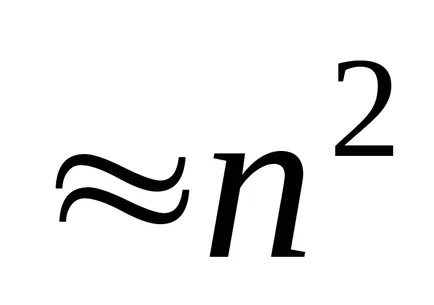
rotunjire eroare pentru metoda iterativă mai puțin.

sisteme mari de ecuații nu pot fi rezolvate exact folosind metode directe.