Metode de optimizare într-o dimensiune mare a problemei
Metoda de agregare bazată pe descompunerea în o probleme la scară largă
bazat pe agregarea metodei de descompunere în probleme de programare neliniare
sisteme de descompunere
Principiul de descompunere (sau cum este numit, principiul descentralizării) este partiționarea sistemului în subsisteme având proprietăți dorite. Această metodă este folosită pentru justificarea ierarhică de construcție a sistemelor complexe, în special pentru studiul diferitelor modele de interacțiune între nivelurile între nivelul sistemelor economice pentru rezolvarea sarcinilor de control și planificare operaționale.
In aplicarea la problemele de descompunere a optimizării este de a împărți sarcina principală în subactivități dimensiune semnificativ mai mică, care poate fi rezolvată prin mijloacele existente.
Aceste subsarcini formează primul sistem ierarhic nivel creat în scopuri de calcul.
La primul nivel subactivități sunt rezolvate la conexiuni arbitrare. Determinarea acestor relații este sarcina celui de al doilea nivel.
Lipsa unui organism de control central pentru informații detaliate despre capacitățile de producție ale subsistemelor individuale necesită o structură ierarhică, în care organismul părinte colectează unele informații agregate cu privire la subsistemele sale subordonate și apoi eliberează-l într-o formă sau alta indicație a dorit sau de așteptat de la activitățile lor. După ce am citit aceste instrucțiuni, subsistemul poate direcționa top „contra-planuri“, în care cel mai bun mod care le-au luat în considerare interesele lor.
Pe baza acestor informații, organismul central de adaptare orientările sale, iar procesul se repetă până la acordul final.
O trăsătură distinctivă a multor probleme practice de cercetare este dimensiunea lor mare. În special, la rezolvarea problemelor de planificare optimă pentru dimensiunea matricei constrângerile macro atinge 10 4 -10 5. în această dimensiune metodele clasice de programare matematice (liniare, neliniare, discrete) sunt ineficiente. Ie ne confruntăm aici cu fenomenul de „blestemul dimensionalitatii“ înțelegere R.Bellmana.
Acest lucru a necesitat dezvoltarea unor tehnici speciale, cum ar fi exactă și aproximative destinate problemelor pe scară largă. Cele mai multe dintre aceste metode utilizează ideea de descompunere, care este în dezmembrarea problemei inițiale de dimensiuni mari, găsirea de soluții independente pentru fiecare dintre ele și apoi se leagă aceste soluții particulare în soluția generală a problemei inițiale. Ideea de descompunere în ceea ce privește problema LP a fost formulat G.Dantsigom și Wolf, și mai târziu a fost dezvoltat în D.B.Yudina, B.G.Golshteyna [12] M. Mesarovich, L.Lesdona [31] V.Tsurkova [52], și altele.
Metoda de descompunere Dantzig-Wolfe
G. Danzig în 1960, și metoda de descompunere Wolfe a dezvoltat soluții pentru problemele dimensionale înalte cu o structură specială a matricei constrângere [31].
Această metodă a fost cea mai eficientă pentru rezolvarea problemelor, matricea de constrângere, care are o formă de bloc diagonală, cu un număr mic de variabile. Cu toate acestea, așa cum se arată prin cercetări suplimentare, metoda este aplicabilă pentru LP probleme cu forma generală a unei matrice de asemenea. Metoda corespunzătoare este furnizat D.B.Yudinym și E.G.Golshteynom numit „programare bloc“ [12].
O trăsătură distinctivă a metodei de descompunere este utilizarea unei sarcini de coordonare. care are, în comparație cu originalul, un număr mic de linii și un număr mare de coloane.
Este esențial ca nu este necesar să se precizeze în mod explicit toate coloanele pentru a rezolva problema de coordonare. Ele sunt generate în procesul de utilizare a metodei simplex. O astfel de abordare este numită metoda de generare coloană. Esența ei este după cum urmează. Să fie o problemă tipuri LP:
Să presupunem că o cunoscută XB admisibilă soluție bazică (DBR) și matricea corespunzătoare a vektorovA bază. Să presupunem, de asemenea, că XB a fost găsit de matricea inversă. Apoi, sa găsit în același timp și vectorul ratingurilor relative
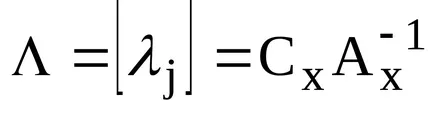
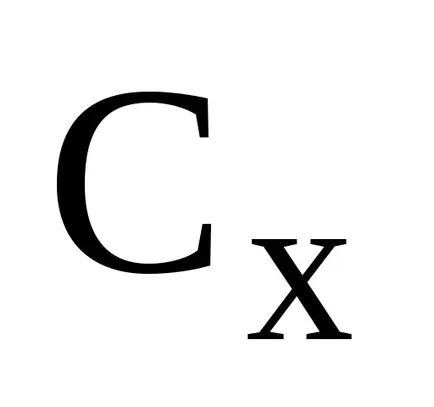
Pentru a determina posibilitatea de a îmbunătăți XB DBD pentru fiecare valoare calculată de evaluare nonbasic vektoraAj:
În cazul în care, soluția inițială poate fi îmbunătățită prin introducerea unei baze variabile XS. Cu toate acestea, în cazul în care există un număr mare de coloane nonbasic (n10 3), prin vectori nahozhdenieS vychisleniyaj pentru toate nonbasic
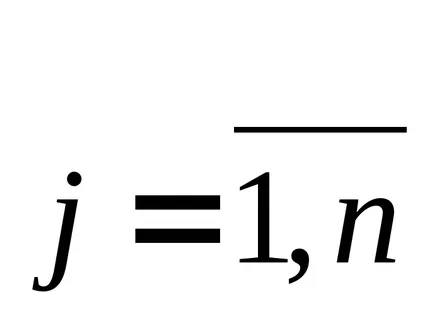
Presupunem că toate coloanele AS selectate dintr-un mnozhestvaS convexe. sistem definit de ecuații și inegalități. Apoi, vectorul coloană care urmează să fie introduse în baza, pot fi determinate prin rezolvarea unei probleme auxiliare de forma:
unde
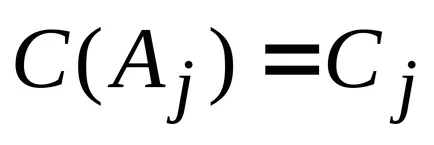
Un astfel de proces este numit de generația coloană. deoarece în soluția problemei (4) este de fapt utilizat doar este generat un număr mic de coloane după cum este necesar.
Acest lucru reduce semnificativ capacitatea de memorie necesară pentru stocarea performanței curente, ceea ce reprezintă un avantaj semnificativ în rezolvarea problemelor pe scară largă.