metoda ortogonalizarea
Gram-Schmidt ortogonalizarea - este o metoda prin care se bazează pe o multitudine de vectori liniar independenți set de vectori ortogonali sau vectori ortonormate construite, și astfel încât fiecare vector sau poate fi exprimată prin combinație liniară a vectorilor. Acest proces poate fi utilizat pentru a obține QR-descompunere. în sistem care vectorii originali formează coloanele matricei originale și coloanele matricei Q sunt obținute dintr-un set de la ortogonalizare vectori. Astfel, spre deosebire de metodele Givens (rotații) și householder (reflecții) bazate pe reducerea matricei lăsat transformări unitare / ortogonale formă triunghiulară, tehnica ortogonalizarea bazată pe reducerea matricei drept nonorthogonal (se poate spune triunghiulare) transformă media unitară / ortogonale .
Baza matematică a metodei
Metoda ortogonalizarea Classic este destul de simplu, cu toate acestea, din cauza instabilității se manifestă în non-ortogonalitatea sistemelor rezultate sunt rar utilizate în practică.
Să presupunem că există vectori liniar independenți. Să presupunem că proiecția unui vector este definit după cum urmează:
unde - produsul scalar al vectorilor.
Produsul scalar a doi vectori în spațiul real k-dimensional este definit ca:
.
Acest operator proiectează un vector coliniar cu vectorul.
Ortogonalitatea vectorilor este realizată în etapa (2).
Gram proces clasic - Schmidt este după cum urmează:
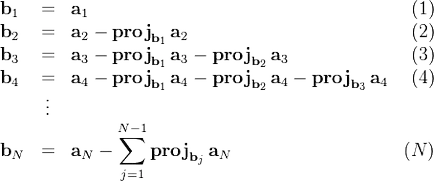
Pe baza fiecărui vector poate fi obținut printr-un vector normalizat (direcția y vectorul normalizat este același ca și originalul, iar norma - unitate). Norma în formula - a fost de acord cu produsul scalar:
Rezultatele procesului de Gram - Schmidt:
- un sistem de vectori ortogonali sau
- un sistem de vectori ortonormate.