Mediana împarte triunghiul

Mediana bisects nu numai latura a triunghiului. Chiar și mediana împarte triunghiul în două părți egale. Să vedem cum această proprietate este utilizat în rezolvarea problemelor.

În primul rând înțelege de ce mediana împarte triunghiul în părți, care sunt pătrat.

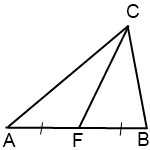
Deoarece ∠AFC și ∠BFC - legate, to∠AFC + ∠BFC = 180ș. Și pentru că formula de aducere sin (180ș - α) = sin α, sin∠AFC = sin (180ș -∠BFC) = sin∠BFC. Deoarece CF mediană împarte partea AB în două părți egale: AF = FB, atunci avem:

Vom continua să ia în considerare sarcinile pentru care este dovedit proprietate este aplicabilă.

La mediană BD ABC triunghi marcat punctul M, astfel încât BM: MD = 3: 1. Găsiți zona triunghiului ABC, în cazul în care aria unui triunghi este egal cu AMD 3 cm².

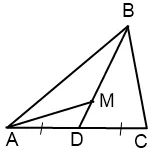
Prin cele de mai sus, zona de triunghiuri ABD și CBD sunt egale. Ne exprimăm aria unui triunghi ABC prin zona AMD a triunghiului: