Manuale 866 - Capitolul 5

unde x x 1. 2. .... xn - unii parametri de optimizare ale obiectului.

Există două tipuri de probleme de optimizare - necondiționate și condiționate.

problemă de optimizare necondiționată este de a găsi funcția efectivă minimă (5.1) variabilelor reale n maxime sau și determinarea valorilor corespunzătoare ale argumentelor.

problemă de optimizare condiționată. sau o problemă cu constrângeri - acestea sunt, în formularea argumentelor pe care restricțiile impuse în formă de egalități și inegalități.

Solutia problemelor de optimizare în care criteriul optimalității este o funcție liniară a variabilelor independente (adică conține variabilele din primul grad), cu constrângeri liniare pe ele, este subiectul programării liniare.

Cuvântul „programare“ reprezintă aici scopul final al studiului - pentru a determina planul optim sau un program optim pe care dintre mai multe variante posibile ale procesului de testare este selectat pe orice bază este cel mai bun, cel mai bun, opțiune.

Un exemplu este problema distribuției optime a materiilor prime între diferitele producții la cel mai mare cost.

Să două tipuri de materii prime din cele două tipuri de produse.

Fie: x 1. x 2 - numărul de unități din primul și cel de-al doilea tip, respectiv; c 1. c 2 - prețul pe unitatea de producție din primul și al doilea tip, respectiv. Apoi, costul total al tuturor produselor vor fi.

Construim un sistem de coordonate rectangulare x 1 Ox 2 domenii de soluții fezabile ale problemei (Fig.11). Pentru a face acest lucru, înlocuiți fiecare dintre inegalitățile (5.5) prin ecuația, vom construi linia de delimitare corespunzătoare:

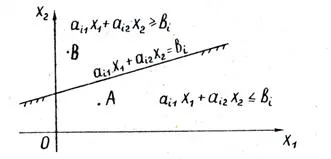
Această linie împarte planul în două jumătăți de avioane. Pentru coordonatele x 1 x 2, orice punct A a unei semiplanului următoarea inegalitate:

și coordonatele oricărui punct în cealaltă semiplanul - inegalitatea inversă:

Coordonatele oricărui punct al liniei de delimitare satisface ecuația:

Pentru a determina care parte a liniei de delimitare este situat la jumătatea planul corespunzător inegalitatea dat este suficient pentru a „testa“ un orice punct (cel mai simplu mod de a punctul O (0, 0)). Dacă substituirea coordonatelor în partea stângă a inegalității este satisfăcută, pe jumătate întors spre la punctul de încercare, în cazul în care inegalitatea nu este îndeplinită, atunci corespunzătoare întoarse pe jumătate în direcția opusă. Direcția semiplan arătat prin hașurare în fig. inegalitățile

corespund semiplanul la dreapta ordonata și pe abscisă.

Cifra construi liniile de delimitare și jumătăți de avioane care corespund tuturor inegalităților.

In general, o parte (intersecția) a acestor semiplanuri va fi o serie de soluții admisibile pentru rezolvarea acestei probleme.

În construcția zonei de soluții fezabile, în funcție de tipul particular de constrângeri de sistem (inegalități) variabile se pot întâlni una dintre următoarele patru cazuri:

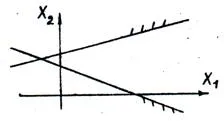
Fig. 12. Zona de soluții fezabile este gol, ceea ce corespunde sistemului de incompatibilitate inegalităților; nu există nici o soluție

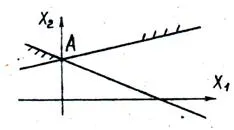
Fig. 13. Câmpul de soluții admisibile reprezentate printr-un singur punct A. soluție unică care corespunde sistemului

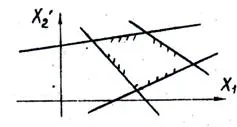
Fig. 14. Zona de soluții fezabile limitate, descrise ca un poligon convex. Un număr infinit de soluții fezabile

Fig. 15. Câmp soluții admisibile nelimitate în forma unei regiuni poligonal convexă. Un număr infinit de soluții fezabile

Reprezentarea grafică a funcției obiectiv

o valoare fixă ​​de R definește o linie dreaptă. și schimbarea R - o familie de linii drepte paralele cu parametrul R. pentru toate punctele situate pe una dintre liniile, funcția R Prien maet o valoare deosebită, astfel încât liniile se numește nivel de linii să funcționeze R.

perpendicular pe liniile de nivel indică direcția creșterii R.

Problema găsirii soluției optime a sistemului de inegalități (5.5), pentru care R funcția obiectiv (5.7) atinge maximul, geo redus metric la definiția din INJ acceptabile soluții depozite de puncte prin care trece la nivelul liniei care corespunde cea mai mare valoare schaya-para- m R

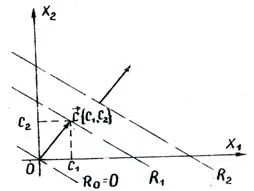
În cazul în care zona de soluții fezabile este un poligon convex, valoarea extremă a R este atins, cel puțin într-una dintre vârfurile poligonului-pneurilor.

Dacă valoarea extremale a lui R este realizată în două vârfuri, aceeași valoare extremă este atinsă în orice punct de pe segmentul de linie care leagă aceste două vârfuri. În acest caz, se spune că problema are o alternativa optima.

În cazul unei regiuni extremum nelegata a funcției Ra nu există sau se realizează într-una dintre nodurile de ambele alternative este optimă.

Să presupunem că doriți să găsiți valorile lui x 1 și x 2. satisfac sistemul de inegalități:

precum și condițiile de nenegativitate.

pentru care funcția:

Înlocuiți fiecare dintre egalitatea inegalităților și să construiască linii de delimitare:

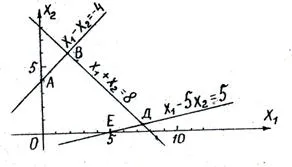
Definiți semiplanuri corespunzătoare acestor inegalități, printr-un punct de „test“ (0; 0). Dată fiind nonnegativeness x 1 și x 2 obținem regiunea de soluții fezabile de această problemă sub forma unui poligon convex OAVDE.

În zona de soluții fezabile pentru a găsi soluții optime, construirea unui vector de gradient

arătând direcția de creștere R.

Soluție optimă corespunde punctului Coordonatele cărora pot fi determinate fie grafic sau prin rezolvarea sistemului de două ecuații care corespund liniilor de delimitare AB și VD B.:

Alocări. Găsiți poziția punctului de extremum, iar valoarea extremă a funcției obiectiv

în funcție de constrângerile date.