funcţia Laplace

Exemplul 2. Un continuu aleatoare X variabilă are o distribuție normală cu următorii parametri: m = 3,  = 4. Găsiți probabilitatea ca rezultatul testului și X. variabila aleatoare) presupune o valoare în intervalul (2, 6); b) are o valoare mai mică de 2; c) să ia o valoare mai mare de 10; g) se abat de la așteptarea printr-o cantitate care nu depășește 2 ilustrează în mod grafic soluția.

Decizie. a) Probabilitatea ca o variabila aleatoare X normală se încadrează într-un interval predeterminat (, ), unde  =  = 2 și 6, este egal cu:

b) Probabilitatea ca o variabila aleatoare X normală are o valoare mai mică de 2, este:

c) Probabilitatea ca o variabila aleatoare X normală va avea o valoare mai mare de 10, este egală cu:

g) Probabilitatea ca o variabila aleatoare X normală se abate de așteptarea de mai puțin  = 2, este:

Din punct de vedere geometric, probabilitatea calculată este numeric egală cu suprafața hașurată sub curba normală (vezi. Figura 6).

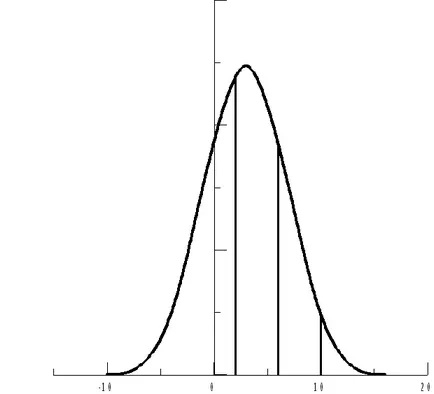
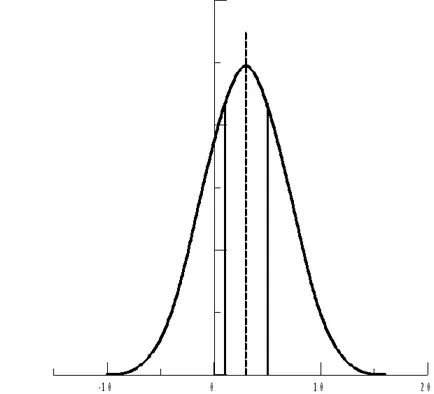
Fig. 6. Curba normală pentru variabila aleatoare X

Exemplul 3. Produs Diametrul arborelui de măsurare fără (un semn) erori sistematice. Erori de măsurare aleatoare supuse unei distribuții normale, cu o deviație standard de 10 mm. Găsiți probabilitatea ca măsurarea se face cu o eroare care să nu depășească în valoare absolută de 15 mm.

Decizie. Așteptarea eroarea aleatoare este zero m = 0. Apoi, probabilitatea ca o variabilă aleatoare X normală se va abate de la speranța de mai puțin  = 15, egal cu:

Exemplul 4. Mașina produce granule. Bila este considerată fit dacă deviația X a diametrul bilei de dimensiunea de proiectare a valorii absolute mai mică de 0,7 mm. Presupunând că variabila aleatoare X este în mod normal distribuită cu o deviație standard de 0,4 mm, găsiți numărul mediu de bile se va potrivi între 100 fabricate.

Decizie. Aleatoare X variabilă - o deviere a diametrul bilei de la dimensiunea de proiectare. Așteptările de deviație este zero, adică M (X) = m = 0. Apoi, probabilitatea ca o variabilă aleatoare X normală se abate de la speranța de mai puțin  = 0,7, este egal cu:

Acest lucru implică faptul că aproximativ 92 de minge 100 se va potrivi.

Exemplul 5. Pentru a demonstra regula „3 ».

Decizie. Probabilitatea ca o variabila aleatoare X normală se abate de așteptarea de mai puțin  = 3 . este egal cu:

Exemplul 6. random variabila X este distribuit în mod normal, cu valoarea medie m = 10. Probabilitatea de a lovi X în intervalul (10, 20) este egal cu 0,3. Care este probabilitatea de a obține X în intervalul (0, 10)?

Decizie. Curba normală este relativ simetrică față de linia x = m = 10, astfel încât suprafața delimitată deasupra și dedesubtul intervalelor curbei normale (0, 10) și (10, 20) sunt egale. Deoarece aria de contact cu probabilitățile sunt numeric egale cu intervalul X corespunzător, atunci: