forţele ponderomotive
Plăci de condensatori electrici, sunt încărcate opus, atrași unul de celălalt.
Forțele mecanice care acționează asupra corpurilor macroscopice încărcat nazyvayutponderomotornymi.
Calculăm forțele care acționează asupra ponderomotive plăcile unui condensator plan. Există două opțiuni posibile:
Condensatorul este încărcat și deconectat de la bateria încărcată (în acest caz, numărul de sarcini pe plăci rămâne constantă q = const).
Când eliminați o placă de condensator de cealaltă lucrare se face
datorită căreia energia potențială a sistemului crește:
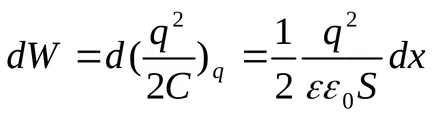
În același timp, dA = dW. Asimilarea laturile dreapta ale acestor expresii, obținem
În acest caz, atunci când diferențierea între plăcile au devenit evidente distanța x.
Condensatorul este încărcat, dar nu este deconectat de la baterie (în acest caz, atunci când se deplasează una dintre plăcile condensatorului este menținută tensiune constantă (U = const). În acest caz, pentru a scoate o singură placă de celălalt câmp potențial condensator de energie scade, deoarece există o taxă „scurgere“ cu plăci, așa
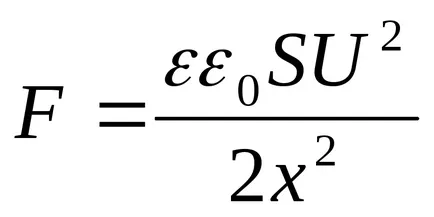
Expresia rezultată coincide cu formula
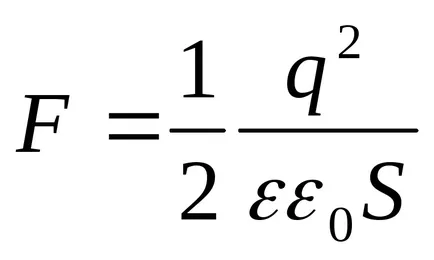
Câmpul este uniformă. Puterea câmpului condensator este egal cu
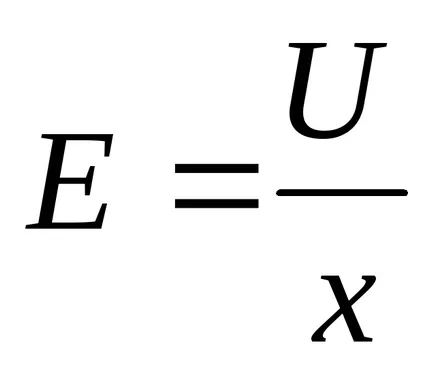
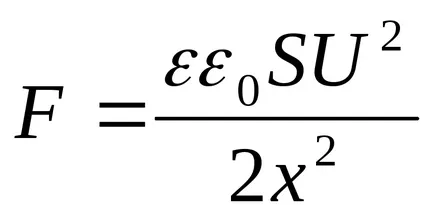
Aceste forțe acționează nu numai pe placa. Deoarece placa, în presă rândul său, pe izolator, plasată între ele și deforma aceasta, presiunea este produsă în dielectric
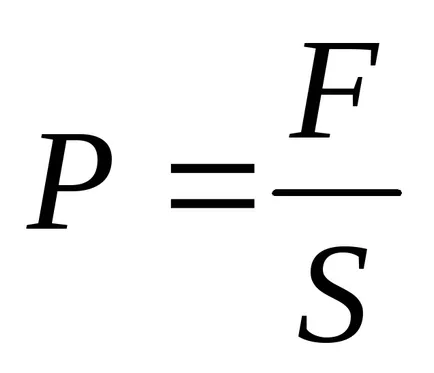
(S - suprafața fiecărei plăci).
Presiunea care apar în dielectric precum
Exemple de rezolvare a problemelor
Exemplul 12. 5.K plăcile condensatorului plan de aer se aplică o diferență de potențial de 1,5 kV. plăci pătrate 150sm2i este distanța între ele de 5 mm. După deconectarea condensatorului de la sursa de tensiune la spațiul dintre plăcile de sticlă lipite (ε2 = 7) .Opredelite:
1) diferența de potențial dintre plăci după aplicarea dielectric; 2) capacitatea condensatorului înainte și după izolator; 3) Densitatea sarcinii de suprafață pe plăcile înainte și după introducerea dielectricului.
Având în vedere. U1 = 1,5 kV = 1,5 ∙ 10 3 V; S = 150cm 2 = 1,5 ∙ 10 -2 m 2; ε1 = 1; d = 5mm = 5 ∙ 10 -3 m.
Decizie. deoarece
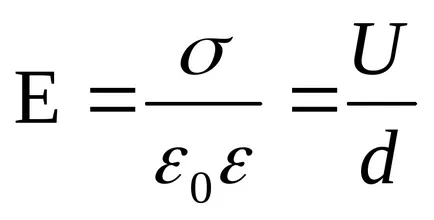
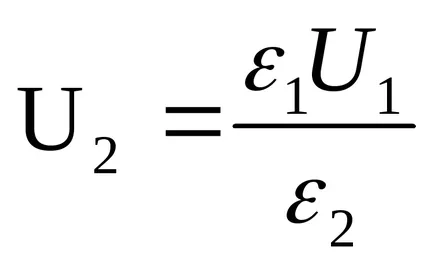
Capacitatea condensatorului înainte și după introducerea dielectrice
plăci Bolt după ce a fost deconectat de la sursa de tensiune nu este schimbat, adică, q = const. Prin urmare, densitatea de încărcare de suprafață pe plăcile înainte și după introducerea dielectrice
Exemplul 12.7. Decalajul dintre plăcile unui condensator plan este umplut cu o anizotrop ε constantă dielectrică, care variază într-o direcție perpendiculară liniar spre plăcile ε = α + βh din ε1do ε2 altfel ε2> ε1. Suprafața fiecărei distanță obkladkiS între nimid. Găsiți capacitatea condensatorului.
Decizie. pronitsaemostε Dielectric variază liniar. ε = α + βh unde x este măsurat de la electrod, care este constant ε1. Având în vedere că ε (0) = ε1. ε (d) = ε2. obținem dependența
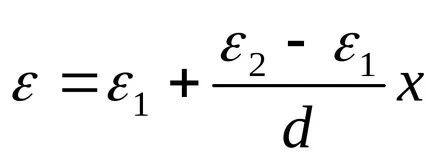
capacitatea condensatorului va fi egal
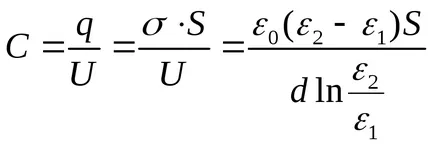
Exemplul 12.7. Între plăcile unui condensator plan, încărcat la o diferență potentsialovU. paralel cu plăcile cele două straturi de dielectric plasate. Grosimea straturilor și dielectricilor permitivitate respectiv ravnyd1, d2, ε1, ε2. Se determină intensitatea câmpului electrostatic în straturile dielectrice.
Decizie. Tensiunea pe plăcile condensatorului, având în vedere că domeniul în cadrul fiecăreia dintre straturile dielectrice este uniform,
deplasare electrică în ambele straturi dielectrice în același mod, astfel încât să putem înregistra
De la expresii (1) și (2) găsi dorit
Din formula (2) rezultă că
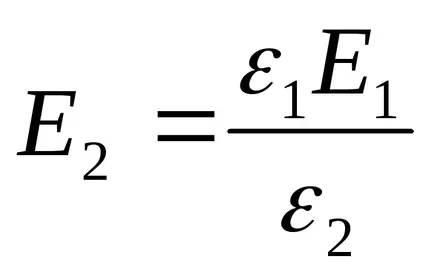
Exemplul 12.7. Zona plastinSploskogo condensator este 100cm2. Spațiul dintre plăcile este umplut cu două straturi de dielectric strâns - placa mica (ε1 = 7) tolschinoyd1 = 3,5 mm și parafină (ε2 = 2) tolschinoyd2 = 5 mm. Se determină capacitatea condensatorului ..
Decizie. capacitatea condensatorului
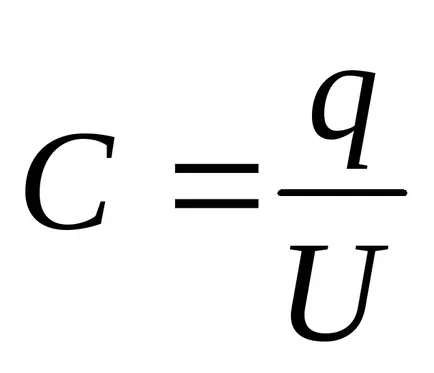
unde = - taxa pe plăcile condensatorului (- suprafața densitate de încărcare pe plăcile); = - plăci diferență de potențial, egală cu cantitatea de stres pe straturile dielectrice: U = U1 + U2. atunci
U1 și U2 Voltages vor găsi formulele
în care E1 și E2 - intensitate câmpului electrostatic în primul și al doilea strat dielectric; D - deplasare electrică în dielectrici (aceeași în ambele cazuri). Având în vedere că
Și formula dată (2), din expresia (1) găsi capacitatea dorită a condensatorului
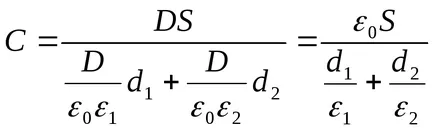
Decizie. Într-o conexiune serie de condensatoare de taxe toate plăcile sunt egale în mărime, așa
Tensiunea pe condensator
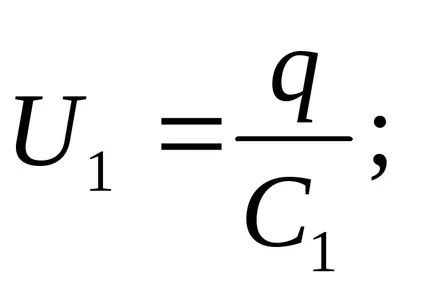
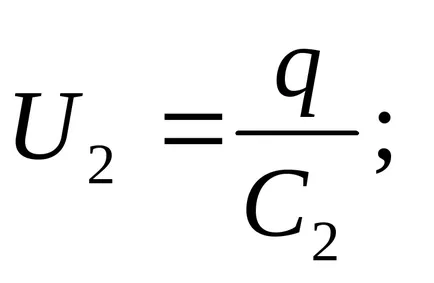
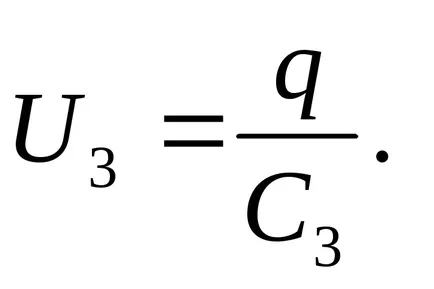
EMF este suma tensiunilor sursă din fiecare dintre condensatori serie conectate:
La conectarea insumata a capacitate de reciproce a fiecăruia dintre condensatoare:
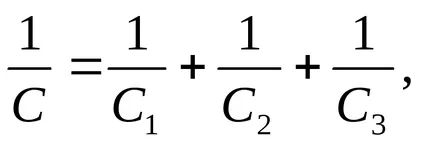
În cazul în care capacitatea dorită de condensatoare
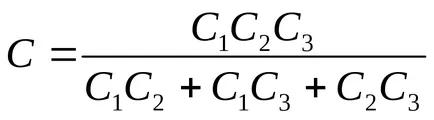
Exemplul 12.7. condensator de aer Două plan de aceeași capacitate sunt conectate în serie și sunt conectate la sursa de EMF. Cum și cât de multe ori pentru a schimba taxa de condensator, în cazul în care una dintre ele este cufundat în ulei, cu o constantă dielectrică ε = 2,2.
Decizie. La conectarea taxele de condensatoare ambele condensatoare sunt egale în mărime. Înainte de scufundare în dielectric (în ulei), taxa fiecărui condensator
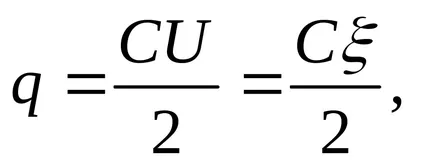
unde ξ = U1 + U2 (o conexiune serie de condensatoare CEM sursă de tensiune egală cu suma fiecăreia dintre condensatoarele).
După imersia unuia dintre condensatori din taxele dielectrice condensator din nou identice și, respectiv, în primul și al doilea condensator sunt
(Luate în considerare faptul că ε1 = 1), în cazul în care, dacă luăm în considerare că ξ = U1 + U2. găsi
Despartitor (2) prin (1) pentru a găsi raportul dorit
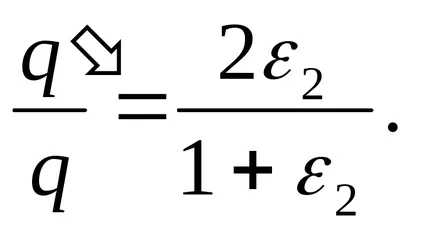
răspundă:
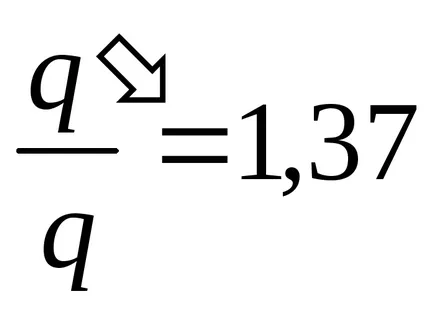
Exemplul 12.7. capacitivitatea condensatoarele C sunt conectate la fiecare așa cum este indicat în ris.a. determină capacitatea de conectare Sobschetogo de condensatoare.
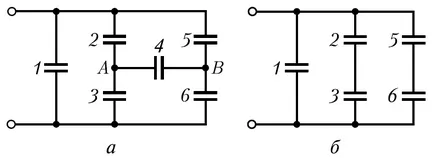
Acest mod schematic trei ramuri paralele, dintre care două cuprind două condensatoare de serie incluse
EXEMPLUL 12.7.Plosky Capacitatea de aer condensatorul C1 este încărcat la 4PF = diferența potentsialovU1 = 100V. După deconectarea condensatorului de la distanța sursă de tensiune între plăcile condensatorului a crescut de două ori. Definiți: 1) diferența plăci potentsialovU2na condensator după razdvizheniya; 2) activitatea forțelor exterioare plăcilor razdvizheniya.
Decizie. Taxa de armăturile condensatorului când este deconectat de la sursa de tensiune nu este schimbat, adică, Q = const. prin urmare
unde C2 și U2 - și containerul respectiv diferența de potențial între plăcile condensatorului după tartinabile lor.
Având în vedere faptul că capacitatea condensatorului plat
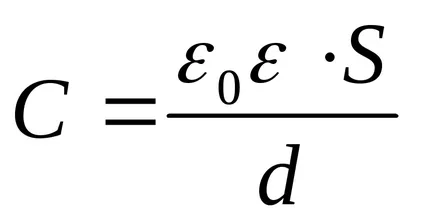
După deconectarea condensatorului de la sistemul sursă de tensiune de două plăci încărcate pot fi considerate ca fiind închise, pentru care legea de conservare a energiei: O lucrare de forțe externe este egală cu energia schimbării sistemului
în care W1 și W2 - respectiv domeniul energetic condensator în stările inițiale și finale.
Având în vedere că
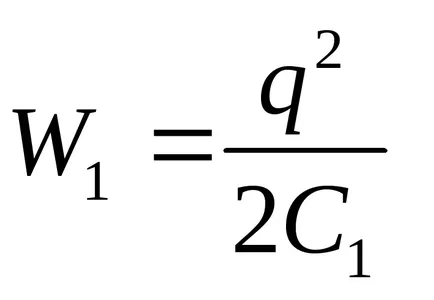
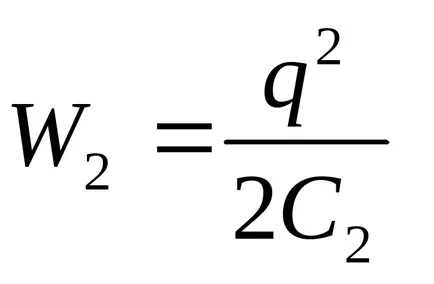
EXEMPLU 12.7.Sploshnoy dielectric bilă radiusomR = 5cm uniform încărcat cu densitatea aparentă ρ = 5nKl / m3. Se determină energia unui câmp electrostatic, închise în spațiul din jurul mingea.
Decizie. Teren mingea este încărcat simetric sferic, astfel încât densitatea de sarcină spațială este aceeași la toate punctele situate la distanțe egale de centrul bilei.
E
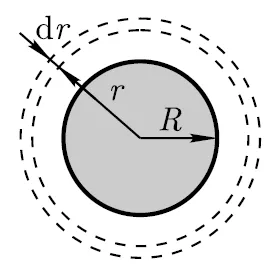
unde dV = 4πr 2 dr (r - raza stratului elementar sferic; dr - grosimea acestuia);
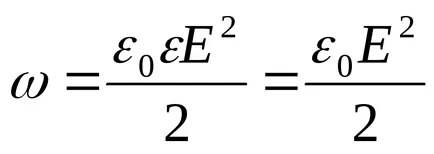
Intensitate E găsi teorema lui Gauss pentru câmp într-un vid, și într-o suprafață închisă selectați mental raza sferei r (vezi. Figura). În acest caz, întreaga suprafață interioară a taxei bilă este adjudecată care generează câmpul respectiv, și prin teorema lui Gauss,
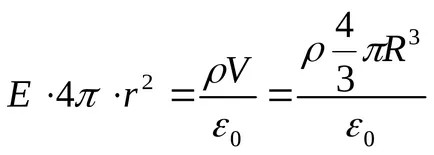
Înlocuind aceste expresii în formula (1), obținem
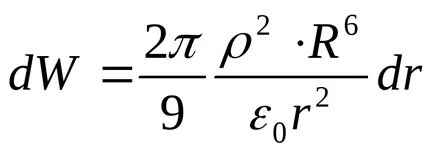
Energia conținută în minge spațiu ambiental,
Răspuns. W = 6,16 ∙ 10 -13 J.
EXEMPLU 12.7.Ploskomu condensator cu o suprafață ℓ spațierea obkladokSi comunicate zaryadq. după care condensatorul este deconectat de la sursa de tensiune. Se determină plăcile condensatorului forță prityazheniyaFmezhdu, dacă constanta dielectrică a mediului între plăci este egală cu ε.
Decizie. Taxa de armăturile condensatorului când este deconectat de la sursa de tensiune nu este schimbat, adică, q = const. Să presupunem că sub forța de atracție F distanța dintre plăcile condensatorului sa schimbat la d ℓ. Apoi, forța F nu funcționează
Conform legii de conservare a energiei, acest lucru este egal cu pierderea de energie a condensatorului, și anume,
în cazul în care, în baza expresiilor (1) și (2), obținem
Înlocuind în expresia pentru energia condensatorului încărcat
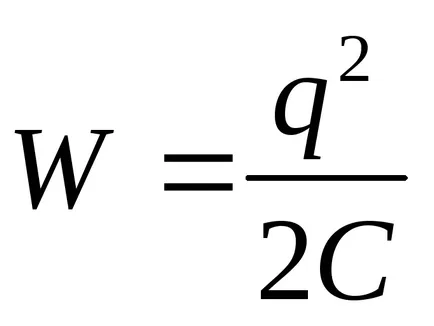
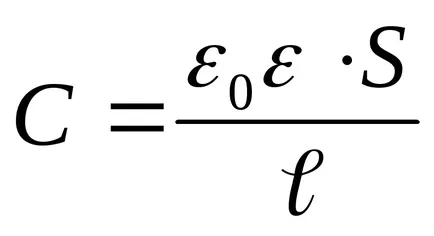
Substituind în (3) din valoarea energetică (4) și diferențierea performante, vom găsi forța de atracție necesară între plăcile condensatorului
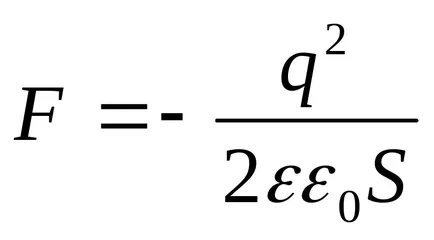
în cazul în care semnul „-“ indică faptul că forța F este forța de atracție.
EXEMPLU 12.7.Plosky zonă condensator ℓ distanța obkladokSi conectat la napryazheniyaU constantă. Se determină plăcile condensatorului forță prityazheniyaFmezhdu, dacă constanta dielectrică a mediului între plăci este egală cu ε.
Decizie. Conform stării problema pe plăcile condensatorului menținute la o tensiune constantă, adică, U = const. Să presupunem că, în forța de atracție F distanța dintre plăcile condensatorului schimbat la dℓ. Apoi, forța F nu funcționează
Conform legii de conservare a energiei, activitatea în acest caz merge pentru a crește puterea de condensator (a se compara cu exercițiul anterior), adică
în cazul în care, în baza expresiilor (1) și (2), obținem
Înlocuind în expresia pentru energia condensatorului
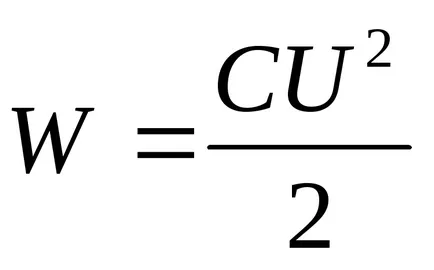
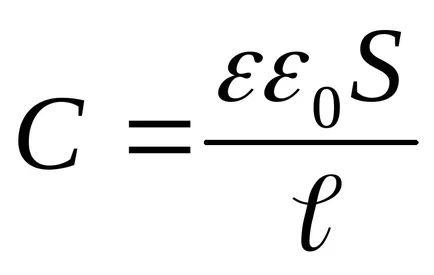
Substituind în (3) din valoarea energetică (4) și diferențierea performante, vom găsi forța de atracție necesară între plăcile condensatorului
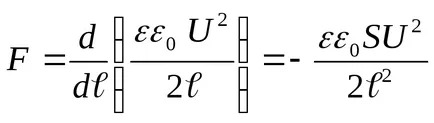
în cazul în care semnul „-“ indică faptul că forța F este forța de atracție.