Ecuații diferențiale în total diferențiale 1

Definiție 8.4. Ecuația diferențială a formei

unde

Se numește ecuație diferențială ordinară.

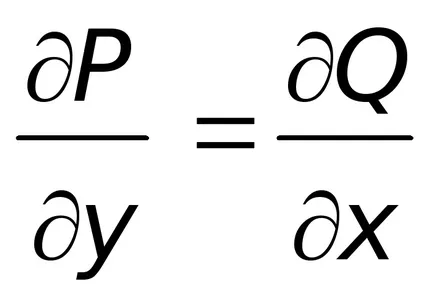
Rețineți că partea stângă a acestei ecuații este diferențial totală a unei funcții

.

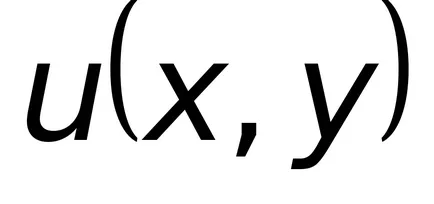
În cazul general, ecuația (8.4) poate fi scrisă ca

În loc de ecuația (8.5) poate fi considerat ecuația

,

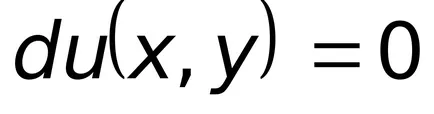
o decizie care are o ecuație integrală generală (8.4). Astfel, pentru o soluție a ecuației (8.4) este necesar să se găsească funcția

. În conformitate cu definiția ecuației (8.4), avem

funcție

Vom căuta, ca funcție, care îndeplinește una dintre aceste condiții (8.6):

unde

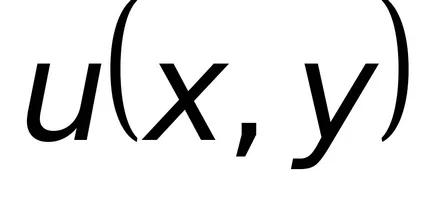
- Funcția arbitrară independentă de.

funcție

Acesta este determinat astfel încât să satisfacă a doua condiție a (8,6)

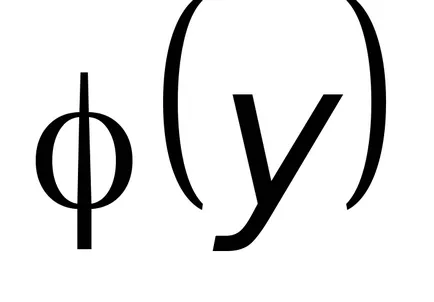
Din expresia (8.7) și este definit printr-o funcție

. Substituind expresiași de a primi o ecuație integrală sursă comună.

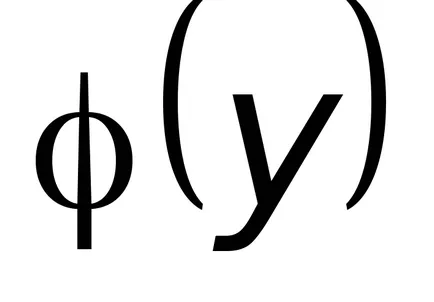
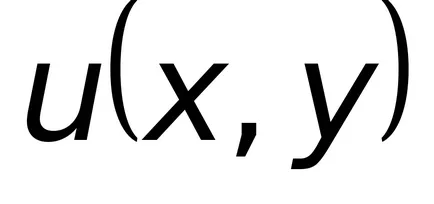
Sarcina 8.3. integra ecuația

Prin urmare, ecuația este ecuațiilor diferențiale de tip în total diferențiale. funcție

Vom fi căutat în formă

;

;

.

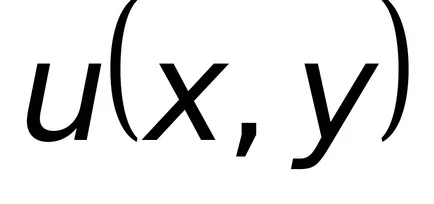
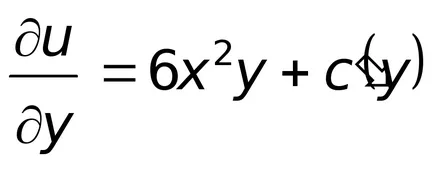
Pe de altă parte,

.

.

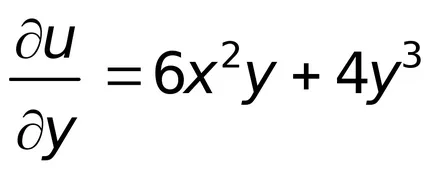
În unele cazuri, condiția

nu poate fi realizată.

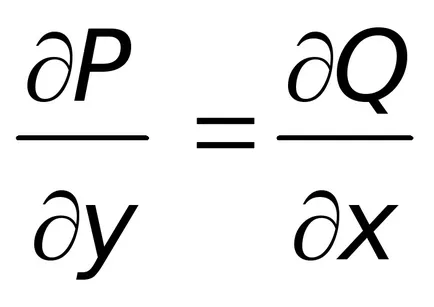
Apoi, aceste ecuații cu tipul considerat se multiplică prin așa-numitul factor de integrare, care, în general, este doar o funcție

sau.

Dacă există un factor de integrare într-o ecuație care depinde numai de

, este determinat prin formula

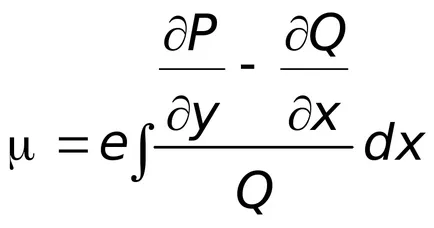
unde raportul dintre

Ar trebui să fie doar o funcție de.

În mod similar, factorul de integrare, care depinde numai de

, definită prin formula

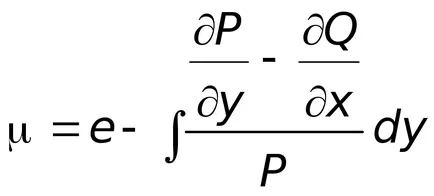
unde raportul dintre

Ar trebui să fie doar o funcție de.

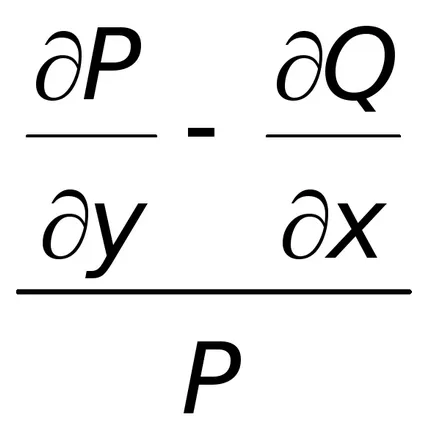
Absența în rapoartele de mai sus, în prima variabilă instanță

, iar al doilea - o variabilă, Este un semn al existenței unui factor de integrare pentru ecuația.

Sarcina 8.4. Adu ecuația la o ecuație cu diferențială totală.

.

.

Subiect 8.2. Ecuatii diferentiale liniare

Definiția 8.5. ecuație diferențială

Se numește liniar în cazul în care este liniar în funcție necunoscută, derivatul săuși nu conține produsul dorit al funcției și derivatul său.

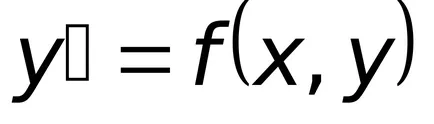
Forma generală a unei ecuații diferențiale liniare este reprezentată prin următoarea relație:

În cazul în care raportul (8.8), pe partea dreapta

, aceasta se numește o ecuație liniară este omogenă. În cazul în care partea dreaptă, aceasta se numește o ecuație liniară neomogen.

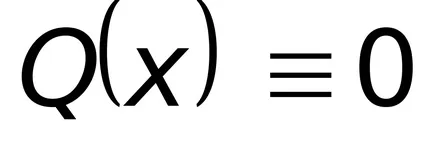
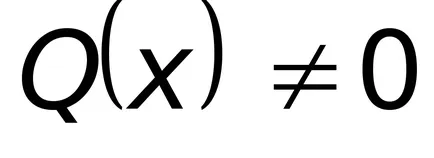
Să ne arate că (8.8) este integrat în cuadraturi.

La prima etapă considerăm ecuație liniară omogenă.

Această ecuație este o ecuație cu mai multe variabile. De fapt,

;

;

/

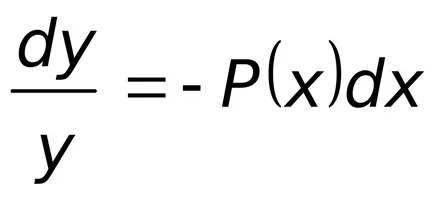
Ultima relație definește o soluție omogenă comună a ecuației liniare.

Pentru a găsi soluția generală a ecuației liniare neomogene metoda de variație a constantei derivatului. Ideea metodei este că soluția generală a ecuației liniare neomogene în aceeași formă ca și cea a soluției omogene a ecuației corespunzătoare, ci o constantă arbitrară

Acesta se înlocuiește cu o funcție, care urmează să fie determinată. Deci, avem:

Substituind în ecuația (8.8) expresia corespunzătoare

și, obținem

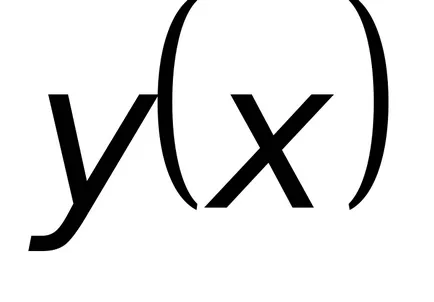
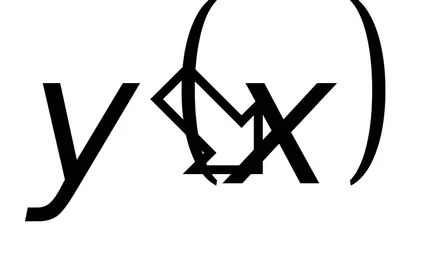
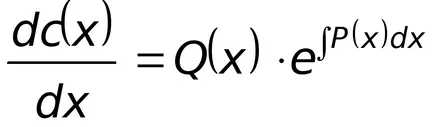
Substituind ultima expresie în (8,9), rezultând un total de ecuații integrale neomogene liniare.

Astfel, soluția generală a ecuației liniare neomogene definita de doua zonă: soluția generală a unei ecuații omogene liniare și o soluție particulară a ecuației liniare neomogene.

Sarcina 8.5. integra ecuația

Astfel, ecuația inițială este de tip ecuații diferențiale eterogene liniare.

La prima etapă vom găsi o soluție generală de ecuații liniare omogene.

;

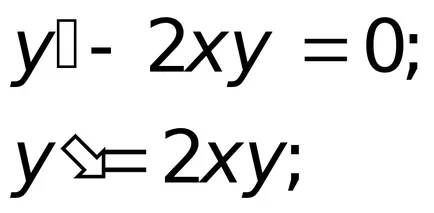
La etapa a doua vom defini soluția generală a ecuației liniare neomogene, care caută luat sub forma

,

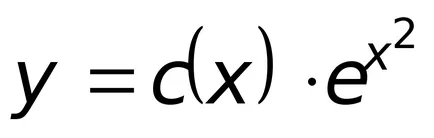
unde

- funcția care urmează să fie determinată.

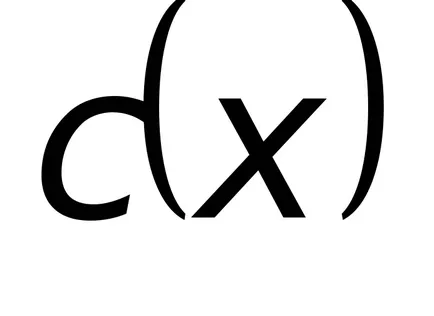
substituind pentru

șiecuația liniară neomogenă de pornire obținem:

;

;

.

Soluția generală a ecuației liniare neomogene ar fi:

.