ecuații diferențiale exacte, exemple, soluții
Părțile laterale stânga ale ecuațiilor diferențiale ale formei, uneori sunt totale diferențiale ale anumitor funcții. Dacă funcția restore din presiunea diferențială totală, integrala generală a ecuației diferențiale este găsit. În acest articol, vom descrie o metodă de restabilire a funcției de diferențială totală, materialul teoretic va furniza exemple și probleme cu soluții detaliate.
Partea stângă a ecuației diferențiale este diferențial total al unei funcții U (x, y) = 0. Dacă condiția.
Deoarece diferențial totală a funcției U (x, y) = 0 este, dacă este îndeplinită condiția se poate argumenta că. În consecință ,.
Din prima ecuație avem. Funcția poate fi găsită prin utilizarea a doua ecuație:

Deci, aceasta va fi găsit funcția dorită U (x, y) = 0.
Găsiți soluția generală a ecuației diferențiale.
În acest exemplu. Condiția este îndeplinită, ca
De aceea, partea stângă a ecuației diferențiale original este diferențial total al unei funcții U (x, y) = 0. Problema noastră este redusă la găsirea acestei funcții.
Deoarece există o diferență completă a unei funcții U (x, y) = 0. atunci. Integrabil ecuație x și y rezultat diferențiabilă. Pe de altă parte, avem de-a doua ecuație. Prin urmare,
unde C - este o constantă arbitrară.
Astfel, integrala totală a ecuației este original.
Există o altă metodă pentru identificarea diferențial totală a funcțiilor sale. Acesta constă în a lua linia integrantă dintr-un punct fix (x0. Y0) la punctul cu coordonatele variabile (x, y). . În acest caz, valoarea integralei nu depinde de calea integrării. Convenabil pentru a lua ca o modalitate de a integra linia întreruptă, legăturile care sunt paralele cu axele de coordonate.
Luați în considerare următorul exemplu.
Găsiți soluția generală a ecuației diferențiale.
Verificați starea:
Astfel, partea stângă a ecuației diferențiale este diferențial total al unei funcții U (x, y) = 0. Considerăm această caracteristică, prin calcularea liniei integrală din punctul (1, 1) până la (x, y). Deoarece calea integrării ia polilinie: o primă porțiune înclinată trece într-o linie dreaptă y = 1, din punctul (1, 1) până la (x, 1). o a doua porțiune de traseu ia linie dreaptă de la punctul (x, 1) până la (x, y).
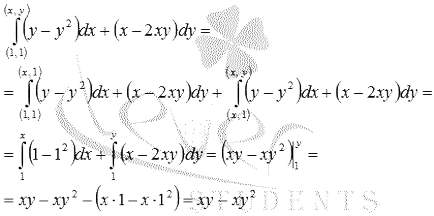
Astfel, soluția generală a ecuației diferențiale este de forma.