Determinarea momet inerție a volantului
Accesorii: instalare; set de mărfuri; line; șubler vernier; cronometru; cântare.
În această lucrare momentul de inerție al roții este determinată prin două metode.
Pe fulie A (sau B) este înfășurat cu firul atașat la acesta o sarcină P (fig. 1). Cădere firului de sarcină unwinds și aduce sistemul (K volant, scripeților A și B, axa C) într-o mișcare de rotație. În acest caz, energia potențială a sarcinii este transformată în energie cinetică a sarcinii, iar energia cinetică a mișcării de rotație a sistemului.
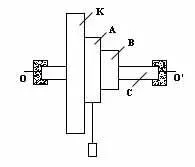
Pe baza legii de conservare a energiei poate fi scris:
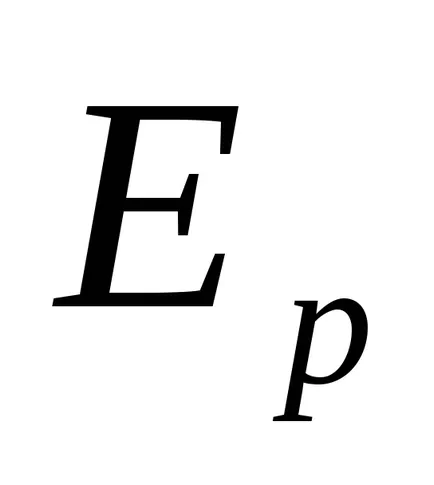
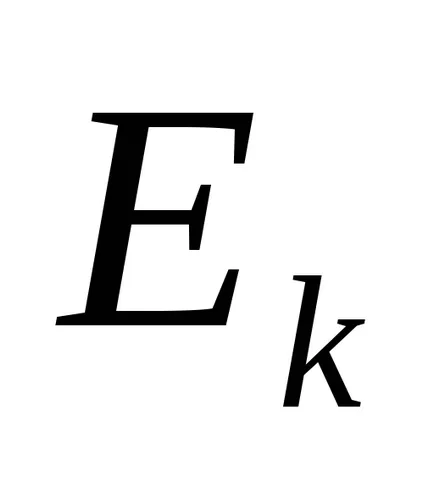
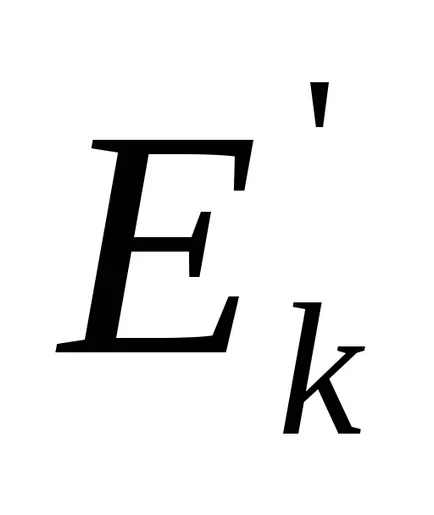
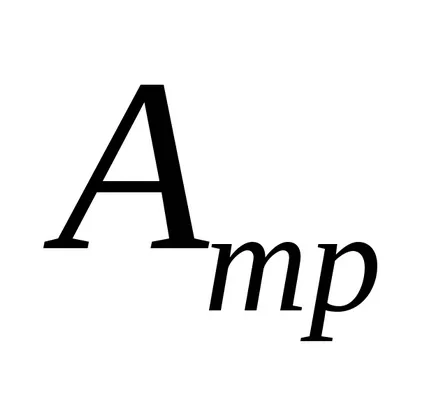
Noi introducem notațiile: m - masa sarcinii; h - înălțimea maximă de ridicare a acestuia; V - viteza sarcinii în poziția inferioară; fulie raza r-; Io - momentul de inerție; - viteza unghiulară în momentul când sarcina ajunge în poziția inferioară.
Apoi ecuația (I) poate fi rescrisă ca:
Deoarece cuplul de frecare nu depinde de viteza de rotație, sistemul va accelerat în mod uniform mișcare.
Cunoașterea gruzat înălțime hi în timpul condusului. ușor pentru a calcula viteza în poziția de jos:
Dacă firul este derulat fără să alunece, viteza liniară de puncte de pe suprafața rolei este egală cu sarcina și viteza
Munca împotriva forței de frecare este proporțională cu numărul de rotații ale sistemului, adică,
unde
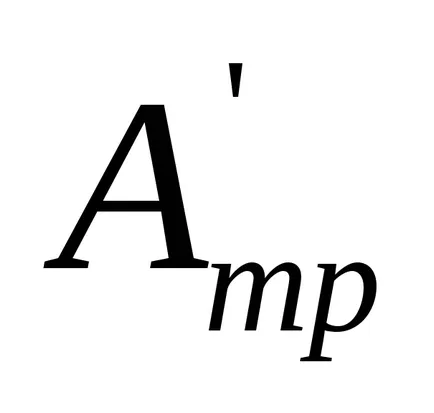
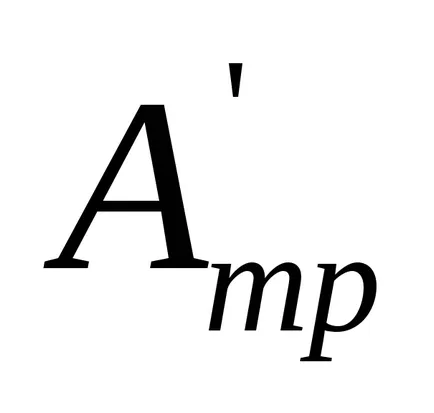
La momentul de a ajunge la poziția inferioară firul de sarcină este separat de scripetele, iar sistemul continuă să se rotească, efectuarea de lucru împotriva forțelor de frecare ca urmare a achiziției de energie cinetică

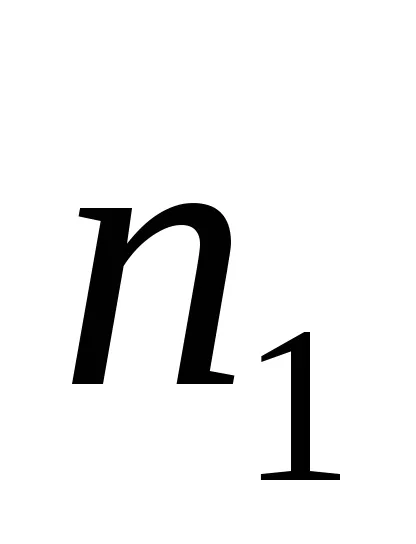
Folosind ecuația (3), (4), (5), (6) și (7) pot fi reprezentate prin (2), în forma următoare:
,
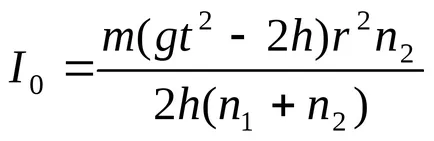
Toate cantitățile din partea dreaptă a acestei egalitati poate fi măsurată în experiment.
Dacă la unele rasctoyaniil din centrul roții atașat la acesta un gruzQ suplimentar (fig. 2), sistemul este convertit într-un pendul fizic.
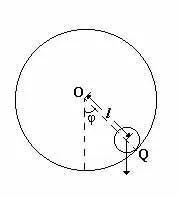
Din poziția scoasă la ieșire de echilibru, pendulul va oscila sub influența momentului gravitațional marfă suplimentar. Neglijând forțele de frecare, putem scrie ecuația de mișcare a pendulului sub forma:
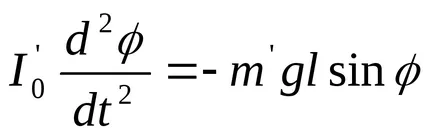
unde
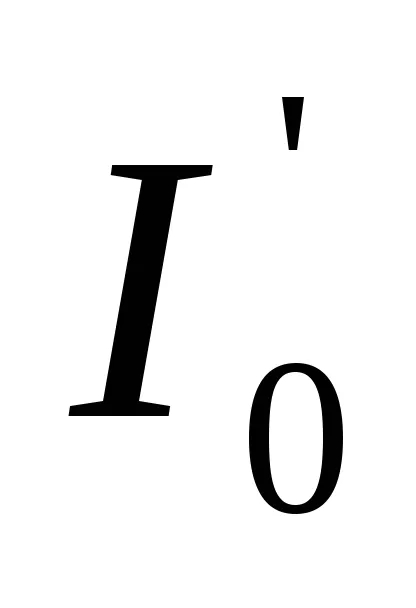
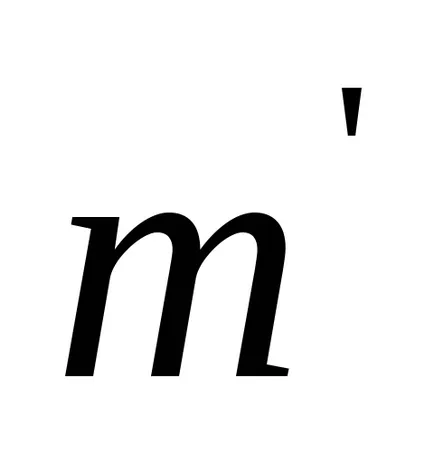
Pentru unghiuri mici
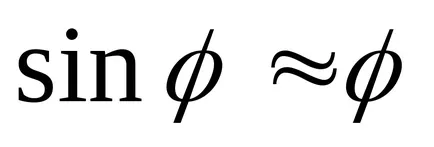
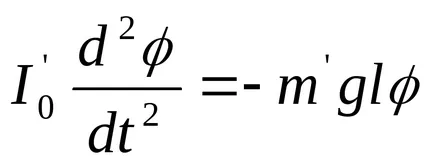
Ecuația (8) reprezintă o ecuație de oscilații armonice cu o perioadă
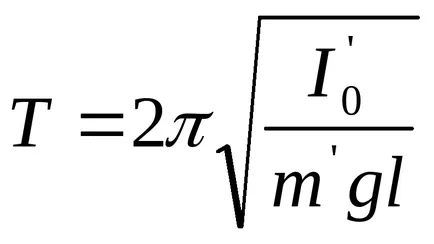
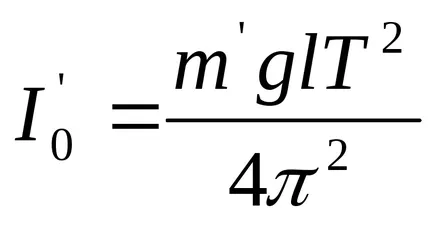
1. Determinarea cuplului de inerție al sistemului.
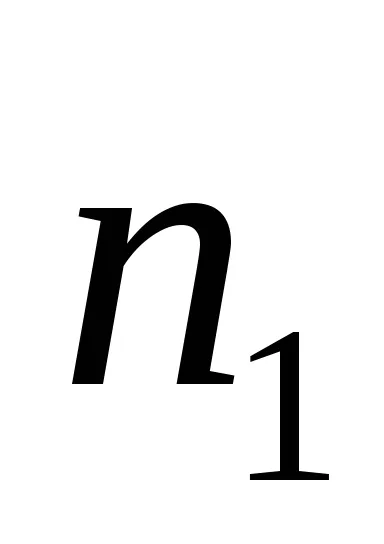
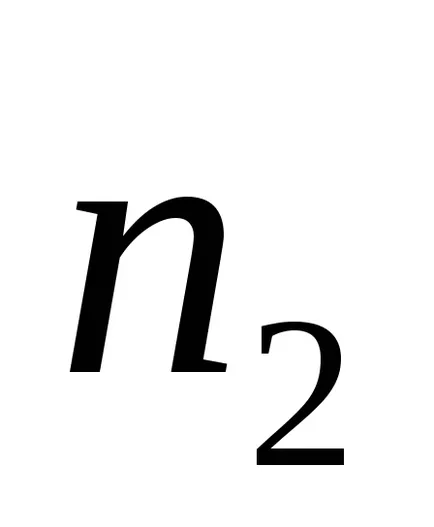
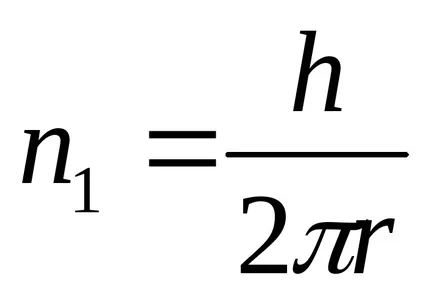
Experimentul a fost realizat pentru 2 încărcături diferite și 2 scripeți diferite raze diferite.
A) m = 249g; d = 7,47 cm; r = 3.75sm; h = 163cm.