Determinarea caracteristicilor temporale și de frecvență ale sistemelor de control automat în MATLAB
Am ales în conformitate cu tabelul de mai sus și întruchiparea funcției de transfer de forma:
Să transformăm această funcție de transfer într-o formă mai convenabilă, prin înmulțirea numărătorul și zamenatl -1:
Scriem funcția de transfer în programul de linie de comandă Matlab cu ajutorul funcției tf. Ca urmare, programul recunoaște datele de intrare ca w funcția de transfer (e):
>> w = tf ([8 iulie -6] [1 3 6 0])
1 s ^ 3 s ^ 3 + 2 + 6 s
Pentru a defini polii pol funcția de transfer introduce comanda (w)
Din rezultatele de calcul al polilor, observăm că sistemul este la limita de stabilitate. Acest lucru rezultă din rădăcina metodei de determinare a stabilității. În acest caz, partea reală este negativă, dar unul dintre rădăcinile are o parte reală zero și o parte imaginară, adică Acesta se află pe axa imaginară.
Pentru a determina zerourile funcției de transfer, comanda scriere zero (w)
Noi folosim etapa de comandă pentru construirea tranzitorie (w)
Procesul de tranziție este instabil. Ie atunci când este aplicat la intrarea unui singur sistem de control al funcției Heaviside, sistemul nu merge niciodată la o singură valoare specificată, și continuă să scadă. O astfel de cădere natură tranzitorie datorită prezenței termenului integral în funcția de transfer:
Pentru a construi un impuls de răspuns, sistemul de intrare va oferi impuls infinit pentru un timp infinitezimal cu comanda de impuls (w). Atunci când se aplică un astfel de semnal, sistemul revine la poziția sa inițială.
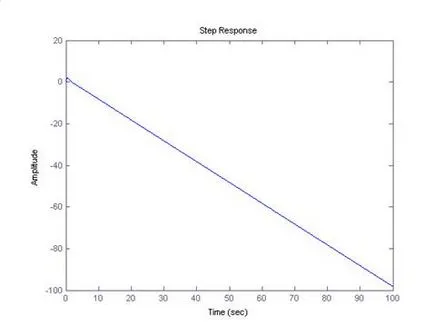
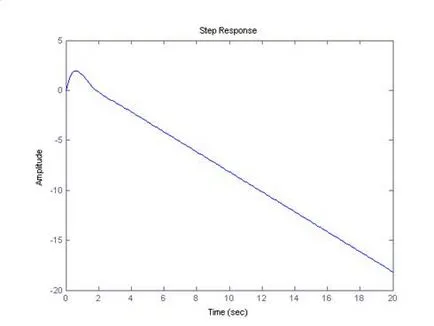
Cifrele arată că natura tranzitorie a incidenței nu se schimbă cu timpul
Noi construim răspunsul la impuls:
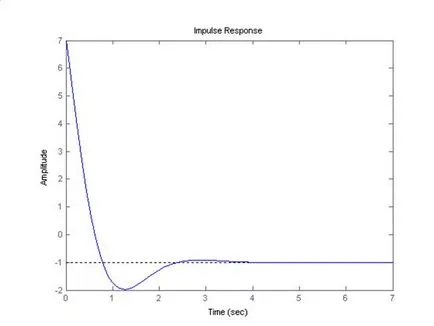
Va oferi de intrare în sistem delta Dirac funcția. Sistemul va funcționa această variabilă de referință, dar nu va fi înapoi în starea de zero, și punctul -1.
Pentru construcția caracteristică comenzii utilizare Bode logaritmică amplitudine-frecvență (w)
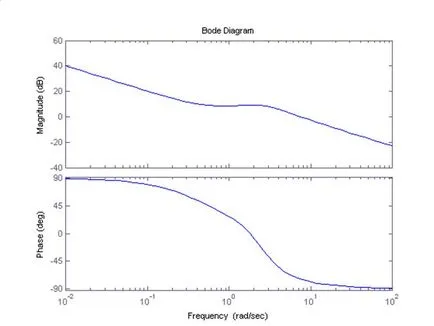
Privind la diagramă, LACHH traversează linia 0 dB / decadă, iar LFCHH - deasupra liniei de -180 de grade, ceea ce indică prezența unei marje de stabilitate în amplitudine, dar nici o marjă de fază.
Pentru construcția APFC răspunsului faze amplitudine sau locusul Nyquist utilizați comanda Nyquist (w). Izvor de falie nu acoperă punctul (-1, j0), ceea ce indică faptul că sistemul de control după circuitul feedback-ul va fi stabil dacă este în poziția deschis, de asemenea, are un caracter stabil.
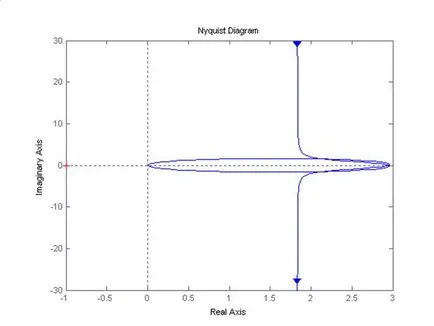
Concluzie: Sistemul este la limita de stabilitate și pentru a deveni durabil, este necesar să intre autoritatea de reglementare (pentru a compensa componenta integrantă necesară pentru a include o proporțională și diferențiator suplimentare)