Definirea momentul de inerție al cilindrului și coeficientul de frecare la rulare, platforma de conținut

Lab N 6

Definirea momentul de inerție al cilindrului

și coeficientul de frecare la rulare

Determinarea experimentală a momentului de inerție al cilindrului și o sferă, compararea momentului de inerție obținută experimental și teoretic.

2. Teoria materiei

A. Momentul de inerție al punctului material este determinat de produsul masei sale și raza pătrat de girație:

La diferite puncte ale corpului reale sunt la distanțe diferite de axa de rotație, astfel încât sunt cuprinse toate momentele de inerție ale punctelor de masă:

unde dm - infinit masa mică a elementului de corp solid.

Deoarece m = Rv, unde r. - densitate Matter, V - volumul corpului, apoi d m = r × dV, unde dV - volumul elementului de corp.

Apoi, cu formula (2) ia forma:

Ca un exemplu, ia în considerare cuplul de ieșire al discului omogen de inerție față de o axă perpendiculară pe planul discului și care trece prin centrul său (Fig. 1).

Am împărți discul în straturi groase dr inelare. Toate punctele de un singur strat va fi la aceeași distanță față de axa egală cu r.

Volumul unui astfel de strat este:

DV = o 2prdr x, unde - grosimea discului.

Condu omogen, r = const.

Conform ecuației (3) avem:

În final, discul care intră în masa m, egală cu r densitate în volum în disc p R2, obținem:

Dacă axa (0 ¢ ¢ 0) perpendicular pe disc, dar trece prin marginea ei (Fig. 1), momentul de inerție este definită folosind teorema lui Steiner. Teorema lui Steiner este formulată după cum urmează: momentul de inerție J în raport cu o axă arbitrară este suma momentului de inerție față de o axă paralelă cu acest corp și care trece prin centrul de masă și produs de greutate corporală m pătrat de distanța d dintre axe:

Astfel, ca și d = R, atunci (7)

Derivam omogene momente sfere de inerție față de o axă care trece prin centrul său. Pentru a determina momentul de inerție minge în raport cu axa centrală O împarte în mai multe discuri elementare (dh grosime) Xou plan paralel (fig. 2).

d h = r d j = Rcos j d j, unde r = Rcosj

masa disc elementar de rază r este egală cu:

Momentul de inerție elementar raza discului r dm și la sol în raport cu axa O este egal cu:

Momentul de inerție în raport cu axa O obține, prin însumarea momentelor de inerție ale discurilor elementare și care trece pentru a limita cantitatea de O până la (pentru emisfera).

Pentru un moment de inerție sferă este

Apoi, volumul unei sfere

Ecuația (12) determină momentul de inerție al bilei (sfera) deoarece se rotește în jurul centrului de masă. În cazul în care mingea este rotit în jurul unei axe care nu trece prin centrul de masă, momentul său de inerție este definit de teorema lui Steiner (5).

B. Energia cinetică a unui corp de rotație în jurul unei axe fixe cu skorostyuw unghiulară egală

În cazul în care corpul se rotește, de asemenea, se deplasează înainte, (mișcare plan), energia cinetică este egală cu suma energiei cinetice a translațională și mișcările de rotație:

Determinarea momentului de inerție al mingea este făcută în această lucrare în raport cu timpul de rulare minge cu un plan înclinat (fig. 3).

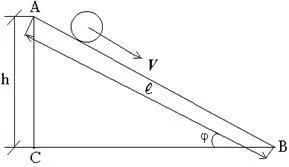
În partea de sus a planului înclinat energia cinetică a mingea este egală cu zero, energia potențială este MGH. La cel mai de jos punct (B), rampa energia potențială a mingea este egală cu zero, energia cinetică a

În plus, o parte din energia merge să lucreze împotriva forțelor de frecare

A = m mg l cosj (15)

unde m - coeficientul de frecare, l - lungimea planului înclinat, j - unghiul de la baza planului înclinat. T. k., Acest unghi este mic, atunci cosj o eroare care să nu depășească 5% poate fi considerată = I, atunci

Conform legii conservării energiei

Dacă nici o viteză unghiulară de alunecare asociată cu relația liniară: w =, unde R - raza de rotație (raza sferei, cilindru).

W Substituind în (17) și a redus la m, obținem:

Ne exprimăm viteza la sfârșitul planului înclinat prin timpul t, și o lungime l:

Formula (18) ia forma:

Prin urmare, momentul de inerție egal cu:

Formula (20) se calculează pentru momentul de inerție al cilindrului și o sferă.

B. frecare rulare

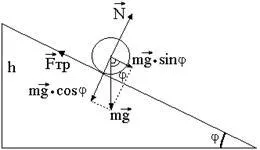
Cilindrul (bila) de rulare pe planul înclinat sub acțiunea trei forțe: forțele de frecare și planul înclinat al reacției (Figura 4.). Reacția în conformitate cu legea a treia a lui Newton este egală cu valoarea absolută a componentei normale a forței. având o magnitudine mg x Sinj.

Frecarea între cilindru și suprafața înclinată are loc la punctele de contact. Deoarece aceste puncte de cilindru la fiecare punct de timp sunt fixate (ele formează axa de rotație instantanee), forța de frecare este forța de frecare (cu role) de odihnă. Alunecare de rulare a cilindrului de-a lungul unui plan să lipsească, cu condiția ca viteza liniară a punctelor de contact este egal cu zero, care la rândul său se efectuează în cazul în care centrul vitezei de masă este în fiecare moment viteza unghiulară w de rotație a cilindrului, înmulțită cu raza cilindrului R

respectiv, accelerația ar centrul de inerție este egală cu accelerația unghiulară înmulțită cu raza:

În aceste condiții, forța de frecare Tp nu depășește o valoare maximă și un cilindru va rula fără alunecarea.

Scriem legea II-lea a lui Newton pentru rulare cilindru (castron) cu planul înclinat:

Cuplu de fricțiune în raport cu axa cilindrului este diferită de zero și egal. Apoi, pe baza legii II al dinamicii pentru mișcarea de rotație a unui corp rigid poate fi scris:

unde J - momentul de inerție al cilindrului în raport cu axa de rotație este egală.

Rezolvarea ecuației 21, 22, 23, constatăm că

Este cunoscut faptul că o lege cu experiență de frecare de rulare este:

unde N - forța de presiune normală, egală, în cazul nostru mgcosj,

R - raza cilindrului, m0 - coeficientul de frecare la rulare.

Prin echivalarea laturile drepte ale ecuațiilor (24) și (25) obținem:

Formula (26) se calculează pentru cilindru.

Pentru coeficientul de frecare mingii de rulare a primi în mod independent:

3. Descrierea metodei de instalare și de măsurare

Instalarea este un plan înclinat cu un jgheab, pe care se mișcă mingea. În partea de sus a mingii (cilindru) este deținut de un electromagnet, cel mai jos punct al jgheabului este un comutator limită care oprește cronometrul. Cronometrul este inclus în U rețea = 220V, împreună cu un electromagnet comutatoare releu în rețea - 24 V.

În funcție de înălțimea planului înclinat variază coeficientul de frecare, care este definit prin formulele (26) și (27).

1. Setați urcare până la £ h 15 cm, se măsoară înălțimea h.

2. Includerea în cronometrul dopul de ieșire și un electromagnet.

3. Setați cadranul de la „magnet“.

4. Setați mingea (cilindru), la partea de sus a jgheabului.

5. Comutați selectorul la „stop ceas“, în cazul în care mingea (cilindru) nu se oprește cronometrul, repeta această experiență. Scoateți timpul cronometrului de numărare t al mișcării bilei (cilindru).

6. Alineatele 3-5 se repetă de 5 ori.

7. Se calculează timpul mediu de rulare.

8. Puneți o durată medie de timp în formula (20). Găsiți-pilot moment de inerție al bilei (cilindru).

10. Se calculează eroarea absolută și relativă prin formulele:

un cilindru și o sferă.

11. Concluzia lucrării.

întrebări de testare

1. Ce este denumit mișcare de rotație ca?

2. Ceea ce se numește momentul forțelor?

3. După cum determinate de momentul de inerție al punctului de material m față de centrul de rotație, distanțate la o distanță r?

4. Ce determină momentul de inerție al corpului?

5. Scrieți formula momentul de inerție al cilindrului, în jurul unei axe care nu trece prin centrul de rotație.

6. Scrieți o formulă care determină energia mecanică totală a corpului atunci când mișcarea avionul?

7. Pentru o formulă determinată momentul de inerție al cilindrului (vas) empiric?

8. Pentru o formulă determinată momentul de inerție al cilindrului (bol) cu un teoretic?

9. Ia-o formulă pentru accelerarea centrului de masă al mingea cu rulare sau planul înclinat, folosind legea de conservare a energiei.

literatură

1. Cursul fizicii. La 3 m. T. 1. Mecanică. Fizica moleculara. - M. Science, 1989.

2, etc -. M. executiv. săpt. 1980

3., etc -. M. Educație, 1985.