Curs de lucru Tovo
2. Produs cartezian. Cardinality.
produs 2.1.Dekartovo de seturi.
pereche ordonat
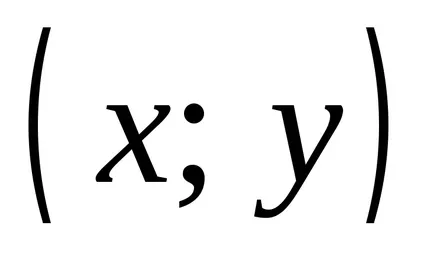
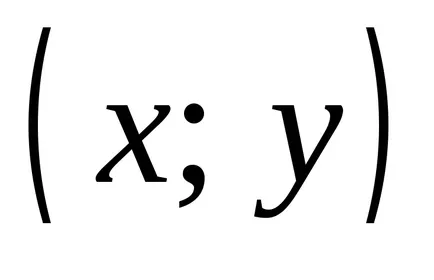
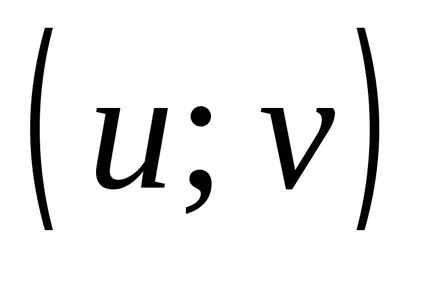
Definiția 2.1. Să A și B - două seturi. produs Direct (cartezian) a două seturi A și B este mulțimea tuturor perechilor ordonate, în care primul element al fiecărei perechi aparține al doilea membru A. B:
.
Primer.. lăsa
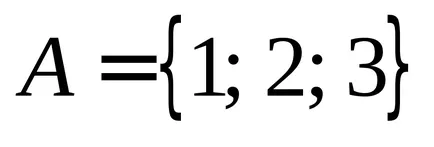
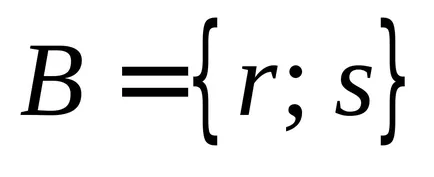
.
.

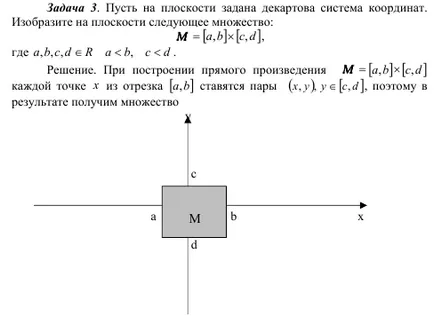
Decizie. Primul set de pus pe axa OX. a doua pe axa OY. Mulțimea tuturor perechilor, adică produs cartezian, punctul reprezentativ al dreptunghiului umbrit, dar fără laturile din stânga și de jos.
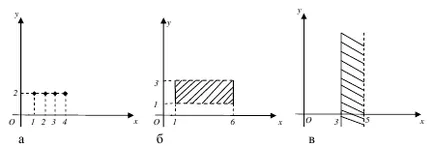
În cazul general, un punct pe planul poate fi definit printr-o pereche ordonată de coordonate, adică cele două puncte de pe axele de coordonate. Prin urmare, planul de coordonate poate fi definit ca
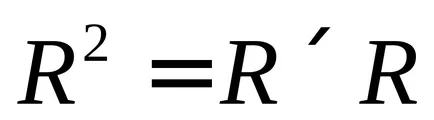
diagramă Venn ce ilustrează o AxB produs cartezian
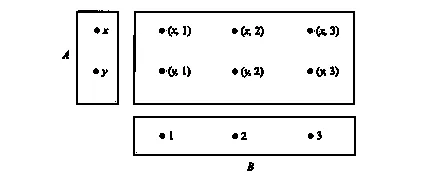
În special, în cazul în care A sau B este gol gol, atunci, prin definiție, A B gol.
Conceptul poate fi generalizat produs direct.
.
Seturile de .I nu sunt neapărat diferite.
Gradul de A este produsul său direct pe sine. denumire:
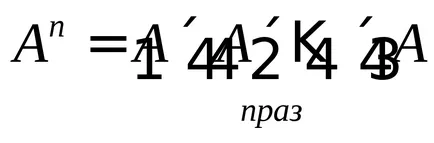
Prin urmare, în general.

Decizie. Bn set este format din secvențe de zerouri și cele de lungime n. Acestea sunt numite șir de biți sau un șir de biți de lungime n.


Se spune că între seturile A și B au stabilit o corespondență unu-la-unu. în cazul în care fiecare element al multimii A corespunde unul și numai un element al lui B și fiecare element al multimii B corespunde unui element al multimii A. În acest caz, se spune că seturile A și Bizomorfny și de a folosi notația A B.
Definiția 2.2. Două seturi A și B sunt echivalente. sau equicardinal. În cazul în care între aceste seturi pot fi instalate o corespondență. În acest caz, scrie: A B. sau A = B , și se spune că seturile A și B au o putere egală.
1) Setul de numere zecimale echivalente cu setul de degete pe mâna persoanei.
2) Setul de numere întregi pozitive (2N) echivalent cu setul de numere naturale (N).
Definiția 2.3. O pluralitate numită finită. dacă este echivalent Jn pentru unii n. unde Jn = 1, 2, ..., n - o multitudine de prime n pozitive întregi.
Determinarea A. 2.4.Moschnostyu set finit care conține elemente k, este numărul de elemente. Ea a indicat A = k. Setul gol este considerat a fi un număr finit de elemente egal cu zero, adică = 0.
Astfel, în cazul în care mulțimea A desigur, adică, A = k. atunci elementele A pot fi întotdeauna renumerotate. care este pus în corespondență cu numărul de articol din segmentul numerelor naturale 1..k de unele proceduri. Prezența unei astfel de proceduri se înțelege atunci când este utilizată înregistrarea A = a1, a2, ..., ak .
Seturile, care nu sunt definitive, numit infinit. În cazul în care o pluralitate de un echivalent cu setul de numere N. naturale și anume Un N. atunci multimea A este numărabilă. Numărabile set A - este un set de toate elementele care pot fi numerotate într-o secvență a1 infinit, a2, ..., an. ..., astfel încât atunci când fiecare element a fost doar un număr n și fiecare număr natural n-ar fi numărul de doar un element al multimii A.
Puterea unui set numărabil este de obicei notată cu
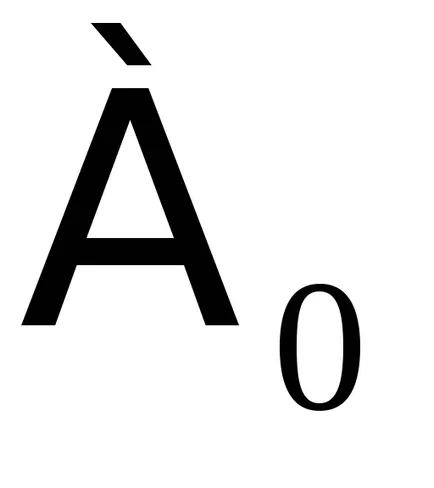

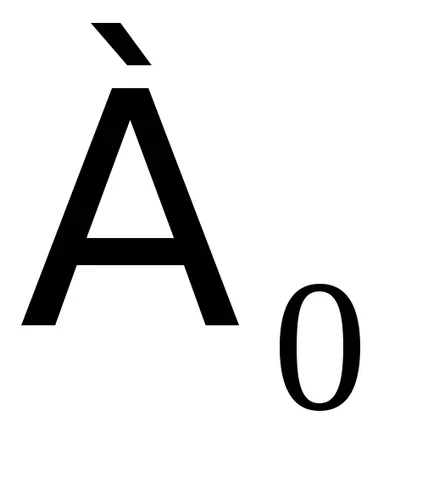
Cea mai mică putere fără sfârșit - puterea setului de numere naturale
Primer.7. Setul de Z - mulțimea numerelor întregi este, de asemenea, numărabil.
Decizie. Luați în considerare mulțimea numerelor întregi Z:
La prima vedere, se pare că acest set nu poate fi renumerotate. Cu toate acestea, această numerotare se poate face prin aplicarea următoarelor truc: nu se deplasează în aceeași direcție, și tot timpul să-l schimbe.
Cu alte cuvinte, vom fi numerotate după cum urmează: numărul 0 va da numărul 1, numărul 1 - numărul 2, numărul 1 - numărul 3, numărul 2 - No. 4, numărul 2 - cameră de 5, etc. Astfel, vom obține o una la o corespondență între Z set și N. Acest lucru înseamnă că setul Z este numărabilă.

O pluralitate numită nenumărat. în cazul în care puterea este mai mare decât puterea setului N. În acest caz, setul se numește o cale A sau un continuum. Puterea continuum este indicată
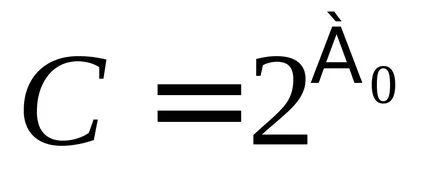
Teorema 2.1. Setul tuturor numerelor reale are cardinalitatea continuum, adică R = C.
plus 2.3.Teoremy și multiplicare.
Principiul incluziune-excludere.
Teorema 2.2. (Teorema plus)
lăsa
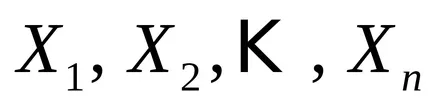
Dovada. Dovedim teorema prin inducție.
.
Inductiv pas. Să presupunem că teorema este adevărată pentru n. Vom arăta că pentru n + 1 este de asemenea adevărat. atunci
Teorema 2.3. (Teorema de multiplicare)
Lăsați un set finit
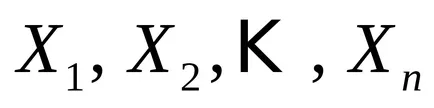
și anume numărul de elemente ale produsului cartezian seturilor este egală cu produsul dintre numărul de elemente factori.
Dovada. Dovedim teorema prin inducție.
Baza de inducție. Fie n = 2. Lăsați setul X1 = A și X2 = B. putere care sunt, respectiv k1 și k2. și anume A = k1. B = k2. Prima componentă a perechilor comandate pot fi alese tehnici k1, a doua - moduri k2. Astfel, există în total diferite k1k2 perechi ordonate. prin urmare,
.
Inductiv pas. Teorema este adevărată pentru n. Arătăm că este adevărat pentru n + 1. Avem:
Primer.. Câte numere întregi între 0 și 1000, care conțin exact un număr de 6?
Decizie. Fie S - set de numere întregi între 0 și 1000, care conține exact o singură cifră 6. Luați în considerare trei subseturi S1. S2 și S3 setului S.
S1 - set care conține un număr care constă dintr-o singură cifră, iar figura 6;
S2 - set conținând număr din două cifre, cu exact o cifră egală cu 6;
S3 - set care conține trei cifre număr cu exact o cifră egală cu 6.
Setul S1 conține doar un singur element - numărul 6. Prin urmare, S1 = 1.
In fiecare element al S2 set care cuprinde 6, are prima sau a doua cifră. Dacă 6 - al doilea număr, atunci există 8 numere diferite, care se va topi în primul rând, pentru că primul număr nu poate fi 0 sau 6. Dacă 6 - prima cifră, numărul 9, din moment ce a doua cifră poate fi 6. Astfel , S2 conține 8 + 9 = 17 elemente, și anume S2 = 17.
Elementul S3 conține 6 ca prima, a doua sau a treia cifră.
Dacă 6 - prima cifră, atunci există 9 opțiuni de a doua cifră și 9 opțiuni de a treia cifră. Conform principiului combinatorie de multiplicare, S3 cuprinde 99 = 81 numere cu prima cifră 6.
Dacă 6 - a doua cifră, există 9 opțiuni de a treia cifră și 8 opțiuni de prima cifră ca prima cifră nu poate fi zero. În consecință, S3 cuprinde 98 = 72 numere ale căror 6 - a doua cifră.
În mod similar, S3 conține 72 numere ale căror 6 - a treia cifră. În consecință, numai S3 conține 81 + 72 + 72 = 225 elemente, și anume S3 = 225.
Deoarece ambele mnozhestvaS1. S2 și S3 sunt disjuncte, atunci
.
Noi pune problema de a calcula numărul de elemente din Uniune
seturi finite
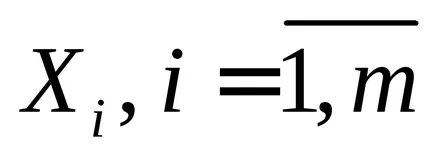
Teorema 2.4. (Principiul Inclusion-excludere).
Pentru seturi finite
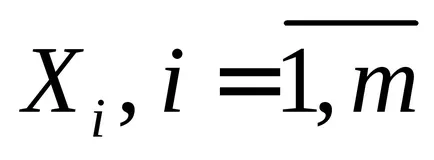
În special, pentru două seturi, această formulă ia forma:
.
Pentru trei seturi de principiu includere-excludere devine:
.
Titlul acestei teoreme accentuează utilizarea incluziuni și excluderea elementelor subseturi succesive.
Primer.. Câte numere întregi pozitive mai puțin de 101, sunt împărțite în 2 sau 3?
Decizie. Fie X - mulțimea numerelor întregi pozitive care sunt divizibil cu 2 sau 3. Luați în considerare două subseturi X1 și X2 set de X.
X1 - setul de numere întregi pozitive care sunt divizibile cu 2. Numărul de elemente sau puterea acestui set este egal cu
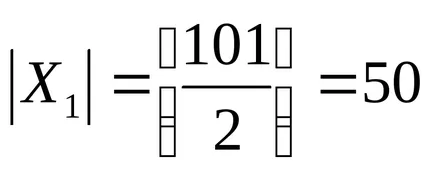
X2 - setul de numere întregi pozitive care sunt divizibile cu 3. Numărul de elemente sau puterea acestui set este egal cu
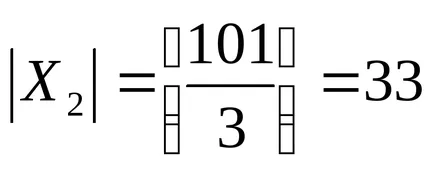
Apoi setul X1 X2 - set de numere întregi pozitive, care sunt divizibile cu 2 și 3 și numărul de elemente sau puterea setului este egal cu
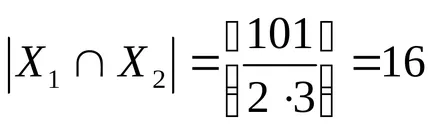
Folosind formula includere și excludere pentru a găsi numărul de elemente de X.
.