Cunoscând curba plan
Să considerăm o curbă continuă arbitrar AB. care nu are puncte de auto-intersecție. Dacă la fiecare punct al unei tangente M, aceasta în timp ce se deplasează TM de la A la B va fi rotit.
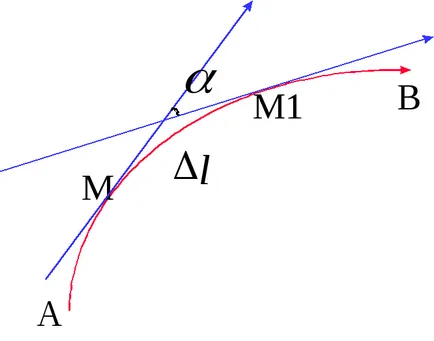
Această curbă este diferită de o linie dreaptă, în cazul în care tangenta este întotdeauna același, și anume, fuzionează cu o linie dreaptă.
Mai rapid transformă o tangentă, curba mai curbat, mai mare de „curbura.“
Noi dăm o definiție matematică a curbură a unei curbe. Luați în considerare un arc arbitrar MM1, la punctele M și M1 comportament retezare. Să presupunem că unghiul dintre ele , acesta nazyv unghiul de adiacenta dugaMM1 = S. Apoi, raportul / S menționate. înseamnă curba curbură AB pe porțiunea MM1. Curbura medie indică unghiul de rotație atunci când se deplasează punctele de tangență M pe unitatea de lungime de-a lungul curbei. Pe diferite părți ale curburii medie a modificărilor curbei. Numai pentru o curbă - curbura medie constanta cercului: DAC = / S = / (R) = 1 / R, cele pentru curbura cercului este reciproca razei.
Pentru a caracteriza cu exactitate curbura curbei în punctul de curbură conceptului este introdus, denota K.
Curbura curbei in TM nazyv limita (daca sesch-a), care tinde să arc curbura MM1 media când curba t.M1 tinde sa M.
K = limS

Limita (1) nu este altceva decât derivatul unghiului de înclinare a tangentei la lungimea arcului și, prin urmare, acesta din urmă limită este o limită pentru raportul funcției increment a creșterii argumentului, adică derivat: K = d / dS, (2).
Astfel, curbura curbei la un punct este derivata a unghiului de înclinare a tangentei la lungimea arcului curbei. Curbura este numărul de non-negativ, așa că, de fapt, K = | d / dS |, (2 „).
Din formula (2) obținem o curbură confortabilă în practică f lu, când curba este definită parametric.
Să presupunem în continuare că funcția (t), (t) au derivati continue ale ordinelor 1 și 2 și xt '= ' (t) t, atunci când este cazul TM
Apoi Ds =, opredelimd.
d =, dS inlocuind, d în (2 „), pentru a ajunge la = |

Dacă curba clară este dată de ecuația y = f (x) se presupune că parametrul t = x, atunci

Dacă curba este dată ecuația polară , atunci presupunem t = obține

Exemplu. Se determină curbura curbei y = SINH în TH = n / 2 -SAMOSTOYATELNO.
§3.Radius, cercul și centrul de curbură. Conceptul de înfășurătoare și involută.
Definiție: Valoarea R, curbura inversă a curbei în punctul K, raza nazyv de curbură a curbei în acest moment este: R = 1 / K. Pentru a direcționa raza de curbură este infinit whith acele linii este un cerc cu o rază infinită.
Pentru circumferința Radus krivizny- este gama de obicei, pentru curbele date în formă parametrică sau ecuații explicite y = f (x) sau raza de curbură este ușor de obținut din formulele (3) - (5). Astfel, pentru y = f (x) R = 1 / K = etc. (propriu).
Am construi o curbă tm la acesta normal și pus deoparte segment concavitate MC = R.
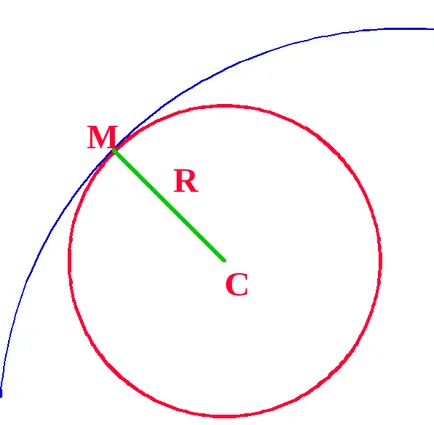
Centrul C Punctul nazyv de curbură în TM, un cerc (cerc) cu centrul C și raza R cerc nazyv (cerc) în linia de curbură TM Curba TM și cercul curbură K-le aceeași curbură, curba deci arc în apropierea M cu o mică eroare poate fi înlocuită cu un arc de curbură a cercului în acel punct.
Fiecare punct al curbei M (L) are propriul centru de curbură punctul C în TM
Locusul centrele de curbură a curbei (L) se numește înfășurătoare sa (L „). (L „) - există, de asemenea, unele curbe. În ceea ce privește (L „) curba inițială (L) este numit involută sau scanare. Acolo formulă. permițând pe ecuația curbei (L) pentru a scrie înfășurătoare ecuație. Și vice-versa.
Aproape înfășurătoare a acestei curbe poate fi construit după cum urmează. Se poate demonstra că fiecare normală pe curba (L) yavl. tangent la înfășurătoare. Prin urmare, construirea unui număr suficient de normale le transporta o curbă care se aplică la toate aceste plic normaley- de normalelor.
Evolventă din înfășurătoare este posibil să se construiască mecanic.

Să îndoit conducător flexibil în mintea înfășurătoare C C0 C0 atașați la capătul firului strâns și trageți pe linie.
În cazul în care acest fir este implementat acum trăgând-o tot timpul la capătul liber, el va descrie o curbă care va evolventă curba C. Deoarece C0 fire pot avea lungimi diferite, involuează la o înfășurătoare poate fi orice număr.