Cunoaște intui, lectura și coordonatele vectorilor

Rezumat: Conceptele matematice de bază legate de definirea poziției obiectului pe plan și în spațiu, cu orientarea și direcția sa, precum și generalizări lor la dimensiunea mai mare a spațiului

Coordonate și vectori

Axa numerică numita linie dreaptă infinită, care sunt definite: punctul O - origine; direcția pozitivă a săgeții; de măsurare la scară (numere de depunere la axa principiu, de multe ori indicând unitate). imaginea Condiționată a liniei reale (fascicul CNC), este prezentată în Fig. 3.1.

Fig. 3.1. număr de linie

Pentru fiecare număr x reale pe axa reală R este definit doar punctul care corespunde valorii sale (reprezentând numărul cu dimensiunea selectată și cadru) și invers, adică totalitatea R și o multitudine de puncte ale axei reale pot fi legate printr-o regulă comună, fără ambiguitate definită, legea.

Exemplu. Numărul 5 pe axa reală corespunde unui punct aflat la distanță de o scală la distanță este de 5 unități de punctul de plecare (punctul de referință 0).

Exemplu. A. Punct de la distanță la o distanță de 3 unități de la începutul scară O origine poate compara numărul 3.

line Number situate în general pe un plan orizontal, la subiect, numita axa x (Ox), un număr de linie situată în general vertical pentru ea, - axa y (Oy) linii .Aceste formează orientarea sistemului fiecărui punct în planul două coordonate sale.

Planul definit de două perpendiculare (sau, așa cum se spune în matematică, ortogonală) a liniei de număr, numit xy planul (xOy).

Fiecare pereche de valori reale (x; y) definește un singur punct M (x, y), în acest plan, care este definit ca punctul de intersecție al perpendiculare liniilor (ortogonale) care trec prin valori axa x Ox și valoarea axei y Oy. Pe de altă parte, fiecare punct (x, y) se poate asocia o pereche de numere reale: x - pe axa Ox și y - axa Oy. Astfel, sistemul definit de două linii perpendiculare numite numerice de coordonate cartezian rectangular sistem în planul (Fig. 3.2).

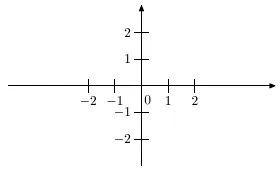
Fig. 3.2. Sistemul de coordonate carteziene în planul

Axelor de coordonate sunt de obicei marcate prin litere.

Ox axa se numește axa x. axa Oy - ordonata axa planul .Aceste axa xOy este împărțit în 4 părți (coordonate unghi sau, așa cum sunt numite, cadranele).

Un set ordonat de trei axe perpendiculare între ele, cu un punct de referință comun pornire (origine) și unitate comună de măsură a lungimii (scala) este un sistem de coordonate cartezian în spațiu .Oboznachaetsya un astfel de sistem Oxyz sau xyz. Ox axa se numește axa x. Oy - y axa. Oz - axa Z.

Mai mult sistemul de coordonate cartezian este adesea folosit și un sistem de coordonate alt convenabil, nu neapărat dreptunghiulară.

Unul dintre cele mai utilizate în mod obișnuit este sistemul de coordonate polare. definind, ca și în sistemul cartezian, poziția neechivocă a punctului în plan cu doi parametri.

Să considerăm un punct de pe O plan (numit pol) și extinzându-se din acest punct jumătatea (numită axa polară). În cazul în care această linie pentru a seta scara și direcția pozitivă, atunci vom defini un sistem de coordonate polare. Poziția punctului M în planul în sistemul de coordonate polare este definită prin două valori numerice: - distanța M din punct de pol, adică și - unghiul format de segmentul OM și direcția pozitivă a axei polare. Notăm punctul cu coordonatele polare în formă. Se crede în general că. Aceste valori sunt numite valoarea principalului. Fiecare punct de pe planul este unic definit prin coordonatele polare. O excepție este singurul punct în care unghiul poate fi arbitrară. Convențional, în acest caz, este luat dintr-un unghi.

Ne găsim relația dintre coordonatele punctului M (x, y) în sistemul de coordonate carteziene și coordonatele sale polare în sistem.

Construirea unui sistem de drept xOy. unde axa Ox coincidentă cu axa polară, O (0, 0) - (. Figura 3.3) originea și direcția pozitivă a acestor axe coincid.

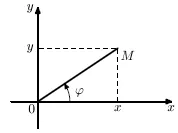
Fig. 3.3. Polar și sistemele de coordonate cartezian în plan

Folosind triunghiuri drepte și funcții trigonometrice, obținem următoarele rapoarte cheie:

Astfel, cunoscând punctul de coordonate polare, coordonate rectangulare pot găsi același punct. Mai mult decât atât, dacă folosim raportul trigonometric de bază și definiția desigur școală tangent (plierea pătrate x y y apoi împărțit la x ..), următoarele relații sunt valabile:

Astfel, dacă știm coordonatele rectangulare ale punctului, putem determina coordonatele carteziene corespunzătoare polare.

Exemplu. Dacă, atunci se obține formula relevantă

De aici derivă sistemul: y = x. x 2 + y 2 = 16 sau mai puțin.

Exemplu. Ecuația cercului cu centrul la origine și raza r într-un sistem de coordonate cartezian, după cum se știe, are forma: x 2 + y 2 r = ecuația 2. cerc în coordonate polare, este de forma

Deci, ecuația este mult mai simplu în minte :. În plus, această ecuație este eliberată din parametrul „exces“, care, în acest caz, este considerat a fi oricare din gama. Lucrul cu obiecte în sistemul de coordonate polare este adesea mai simplu, în practică, topografie, etc. astronomia.

Un sistem de coordonate convenabil în spațiu și este așa-numitul sistem de coordonate sferice. În acest sistem, poziția punctului M (x, y, z) în spațiu este unic determinat de r distanța sa de origine (lungimea segmentului OM), unghiul dintre OM și pozitiv pe jumătate axa Oz și unghiul (între proiecție OM pe planul xOy și pozitiv jumătate axa Ox ( Fig. 3.4).

Să ne determina forma sferică de comunicare și de coordonate carteziene. Conform Fig. 3.4:

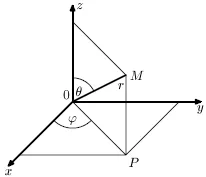
Fig. 3.4. Sferic Sistemul de coordonate