Construiți graficele de funcții, platforma de conținut

2. Cea mai mare parte a „construi grafice de funcții.“ 4

3. Concluzie. 13

4. Referințe. 14

Pe lecțiile algebra am învățat să atragă grafice de funcții elementare: liniară, pătratică, invers proporțional, logaritmică, exponențială, de putere, funcții trigonometrice. In 9m si 10m clasa, am învățat cum să construiască o mulțime de elemente grafice înseamnă de transformări geometrice ale graficelor de funcții de translație paralelă, o traducere de-a lungul axelor de coordonate, de compresie și se întinde de-a lungul axelor de coordonate. Printre aceste reforme, am subliniat construcția metodei adăugarea de grafice. Într-adevăr, multe dintre funcțiile pot fi reprezentate ca suma mai multor funcții:

Ea poate fi exprimată ca suma a două funcții

Funcția poate fi reprezentată ca o sumă de funcții y (x) = x + 2 și graficul fiecărei funcții, suntem capabili de a construi. Apoi, există o problemă: cum de a construi un grafic al funcției, care va fi suma de două funcții. Și astfel: scopul meu eseu pentru a afla regulile pentru construirea graficelor de funcții y = f (x), unde f (x) = q (x) + h (x). Pentru a face acest lucru, am nevoie pentru a obține informațiile necesare cu privire la aceste diagrame.

1. Studiu informațiile privind subiectul în literatura de specialitate, inclusiv cele din manual.

2. Se efectuează funcțiile practice de diagrame care reprezintă suma celor două funcții elementare.

Materialul teoretic pe tema „Adăugarea de grafice de funcții“ Am învățat din cărți: „grafice transformare geometrică a funcțiilor“ și „graficul funcției“ Director. și altele. Din aceste cărți am învățat regulile de adăugare a metodei grafice.

Pe baza materialului studiat, am ajuns la concluzia că o metodă generală pentru trasarea suma a două funcții este aceea că pre-construi două grafice pentru ambele funcții, și apoi adăugați în sus ordonatele acestor curbe, cu aceleași valori ale lui x (la îndemână - la punctele caracteristice ). Punctele obținute construirea calendarului dorit și funcționează cu mai multe puncte de control.

În unele cazuri, construirea unei sume de funcții de grafice pot fi realizate astfel.

Dacă este necesar să complot suma a două funcții, să construiască mai întâi un grafic, o funcție simplă, apoi la programul său parcat-o a doua funcție, care Ordonata reprezentată în funcție de punctele corespunzătoare ale primului program.

Noi construim graficul funcției.

Funcții Plot, termeni și y = x. Apoi se adaugă în sus ordonatele curbelor pentru aceleași valori ale lui x. Ia valoarea x =. 1, 2, 3, ... ordonata .Skladyvaya ambelor grafice pentru fiecare dintre aceste valori ale lui x, obținem punctele A, B, C, D. Prin combinarea lor linie netedă, obține o ramură a funcției graficului (pentru x> 0). Rețineți că funcția impar și graficul acesteia este simetric față de origine, vom construi oa doua ramură generată funcția predeterminată (pentru x <0).

Pentru a studia problema prezenței asymptotes graficului, am acordat o atenție faptului că expresia și a cerut aceeași funcție. Deci, pentru a construi un grafic al funcției, putem construi graficul funcției, iar acestea sunt suma a două funcții.

Pentru a reprezenta grafic funcția este necesar să se stabilească listele ordonate respective și.

Având în vedere funcția ca sumă a două funcții:

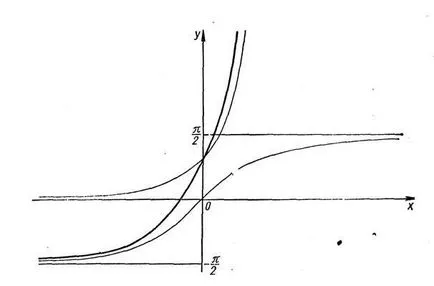
Domeniul a funcției suma: o parte comună a domeniului a funcției termeni, în acest caz [-; ]. Intervalul a funcției suma: [- 1; 1]. Funcția este periodică cu perioada 2p. Punctul caracteristic al graficului verilor fierbinți: punctul de intersecție cu axa x (, 0) (, 0); punctul de intersecție cu axa y (0, 1); Valorile limită funcție sunt egale cu 1; A1 (;) - punctul maxim al unei funcții predeterminate,

A2 (;) - punctul minim al unei funcții predeterminate. La intervale [0; ] Și [; 2p] Funcția crește în monoton [; ] - scade monoton. La [0; ] Funcția Convex pe [; ] - concave [; 2p] - convexe.

Graficul funcției y = sinx + COSX reprezentat în figură.

sunt prezentate exemple de construcție a sumei graficelor de funcții.

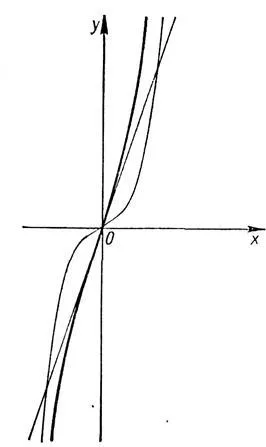
Se trasează funcția y = x2 +.

Graficele functiilor y = x2 și y = cunoscută. Din graficele acestor funcții este clar că graficul y = x2 +. în apropierea punctului

x = 0 aproape fuzionează cu graficul funcției y =. Situat chiar deasupra acestui program, și pentru valori mari de | x | aproape fuzionează cu graficul funcției y = x2. Situat deasupra când x> 0 si dedesubt la x <0. Вычисляя значения функции в нескольких промежуточных точках, видим, что искомый график имеет вид, показанный на рисунке.

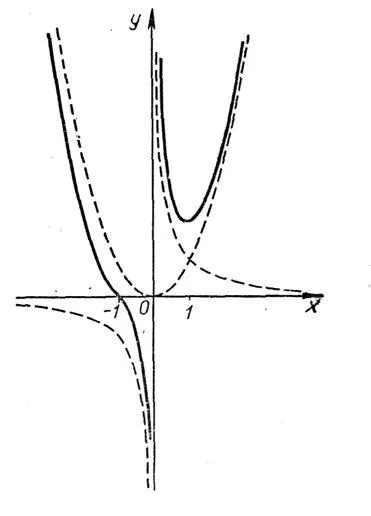
Graficul y = x2 + 4x + 5, puteți construi o varietate de moduri, dintre care trei le cunoaștem:

Graficul functiei este foarte interesant, t. Pentru a. El are o asimptotă verticală la x = 0 și curba asimptotică y = x2, dar este o chestiune de un eseu sau muncă de cercetare pe o temă diferită.

Efectuarea de lucrări abstracte „Construiți graficele funcțiilor“, algoritmul a fost trasarea o altă metodă de transformări geometrice:

1) Trimite această funcție ca sumă a două funcții elementare.

2) Crearea unui tabel de valori ale acestor funcții.

3) Găsiți suma ordonatelor respective pentru aceleași valori x.

4) La acest punct trage un grafic al funcției.

1. „Graficul funcției. Directory“. Editura Kiev, "Naukova Dumka" în 1979

2. „graficele de transformare geometrică a funcțiilor“ Uchpedgiz - 1960 pagina 168.