Construi ecuații predeterminate cardioid în coordonate polare

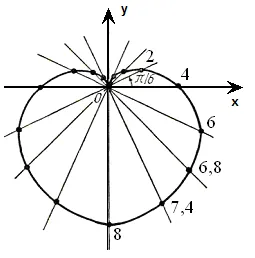
Rezultatele indica Mi Construirea (ρi; φi) în coordonate polare sistem și conectarea lor într-o linie netedă, obține o reprezentare suficient de exactă a cardioidă (figura 4). ◄

Construiți o suprafață de date și de a determina tipul lor (nume):

a) Fie ecuația la forma canonică

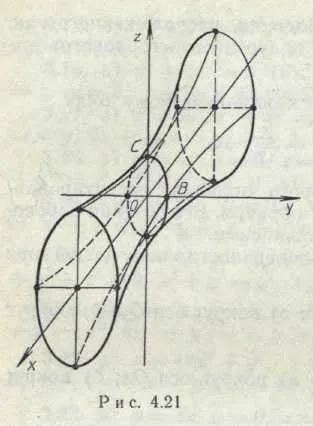
Am obținut ecuația hiperboloidul, situată așa cum se arată în Fig. 5, semiaxes ei "gât" elipsa RH = / 2, OS = 2;

b) Fie ecuația în forma canonică

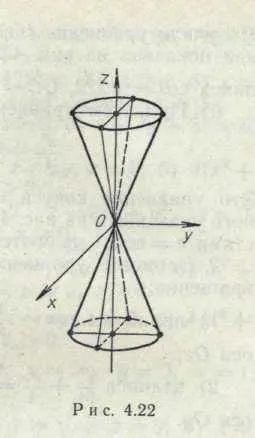
Această ecuație de ordinul doi al conului, orientat așa cum se arată în Fig. 6 mod. His-secțională plane z = const elipse. ◄

(Fig. 5). Hiperboloid (Fig. 6). Cone a doua

Se înregistrează ecuația suprafeței obținute prin rotație:

1) parabolei: a) în jurul axei Oy; b) în jurul axei Oz;

2) a elipsei: a) în jurul axei Oz; b) în jurul axei y.

►1. Ca regulă generală, obținerea ecuației suprafeței de rotație este:

(suprafețe de ordinul a patra algebrici (Figura 7).);

(Paraboloid rotațională (vezi fig. 8)).

A primit de-a lungul axei Oz elipsoid de revoluție (sferoid), secțiunile sale semiaxis majore OA = OB = 8 OS = 2 (Figura 9) aplatizat.

(Oy se extinde de-a lungul axei de rotație elipsoid (Figura 10) :. OA = OC = 2, RH = 8). ◄

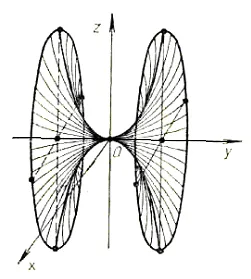
(Fig. 7). Suprafața algebrică a patra comanda

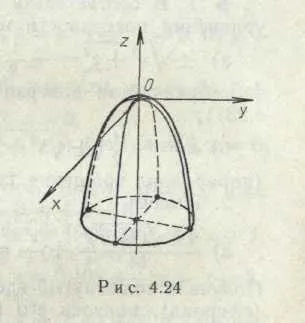
(Fig. 8). paraboloid de revoluție

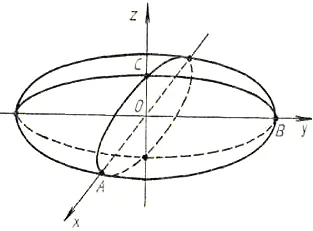
(Fig. 9). elipsoid de rotație (sferoidal) (aplatizat de-a lungul axei Oz)

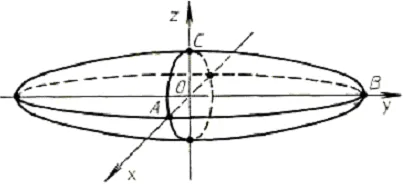
(Fig. 10). elipsoid de rotație (extinzându-se de-a lungul axei Oy)

corp delimitat de aceste suprafețe de pornire:

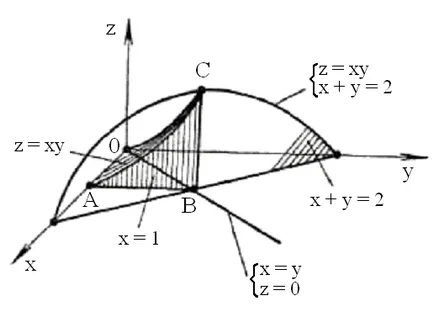
►a) Construcția realizată în Fig. 11: OS - arcul parabolei, care este intersecția paraboloid hiperbolic z = xy cu x = planul y; arc AC - intersecție a z = planul xy suprafață cu x = 1; A (1, 0, 0), B (1, 1, 0), C (1, 1, 1) - punctul caracteristic al corpului;

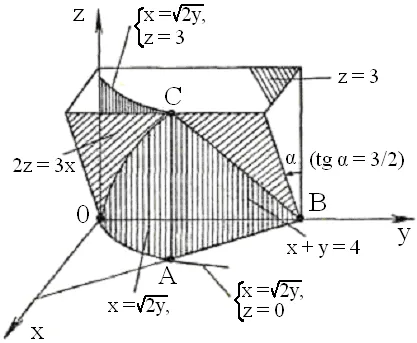
b) Construcția realizată în Fig. 12: OS - arcul parabolei, care este intersecția planului cilindrului parabolic 2z = 3x; A (2, 2, 0),

In (0, 4, 0), C (2; 2; 3); - punctul caracteristic al corpului. ◄

2. Găsiți limitele specificate.

naytiminory factor determinant și algebraicheskiedopolneniyaelementov AI2. prin elementele i-lea rând. 3; 7; -5), B (2, -4, 1). Sarcina 7 Având în doi vectori: = <8; 4; 1>, = <2;–2; 1>. Găsiți vector. și vectori coplanari. perpendicular pe vectorul.

găsi o matrice pătrată) minorelementa; b) algebraicheskoedopolnenieelementa; c). Găsiți un) minorelementa; b) algebraicheskoedopolnenieelementa; c) determinantul, zerourile anterioare, în primul rând. Soluție a) Minoromelementa.

element de matrice. " Definiția. Algebraicheskimdopolneniemelementa aіk matricea A este numită Minor MIK această matrice multiplicată cu (-1) și + la: Algebraicheskoedopolnenieelementa. metodă. Exemplul 1. Găsiți dat det matricea A. Soluție. Transformare.

coloană th; numit minoromelementa. Apoi, prin definiție, luate în considerare (1) - algebraicheskoedopolnenieelementa. apoi (2). operații liniare pe matrici de activitate. Găsiți suma matricelor și a produsului. compatibil, este necesar de a găsi o soluție generală.

Acest factor determinant se numește AIJ minoromelementa. Desemnat minor - Mij. Exemplu: Pentru Naytiminorelementa determinant a12. pe unitate de mai jos și este minoră: Algebraicheskimdopolneniemelementa determinant este numit minor sa luat cu ea.