Construcția de suprafețe în Mathcad și arțar
Mathcad. Construcția de suprafețe.
construcție rapidă este cel mai simplu mod de a construi suprafete. Pentru a face acest lucru:
1. Pe o foaie Mathcad introduceți formula z (x, y): = ...;
2. Selectați comanda din meniul principal „Insert“, „Schedule“, selectați tipul de program „de suprafață“ pe bara de instrumente „Charts“.
3. șablonul grafică tridimensională introduceți numele unei funcții fără argumente.
Construcția de suprafețe pe matricea z.
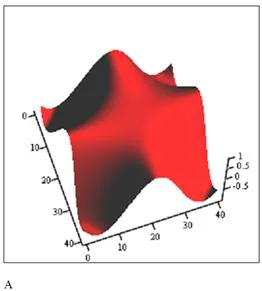
Cea mai suprafață metoda plotting „corectă“, definită prin funcția de două variabile z = f (x, y), este de a umple această funcție valori ale matricei. Astfel rândurile și coloanele matricei sunt interpretate ca abscisă și ordonată. exemplu:
Definirea unei funcții de două variabile z (x, y): (. X y) = cos
Numărul de linii pentru a reprezenta grafic și scara N: = 40 M: = 40
Determinarea indicilor i: = 0..N j: = 0..N
Definirea tablouri și xi x-ordonator: =
În șablon de grafică tridimensională, introduceți numele z matrice:
Construcție folosind funcția CreateMesh.
Formatul unui apel de funcție:
CreateMesh (F. X1, x2, y1, y2, xgrid, ygrid, mesh).
CreateMesh parametrii funcției:
Mesh - numărul de linii în funcție de grila;
F - forma funcției (sau poate fi o formulă sau un vector tridimensional definind fiecare coordonată în formă parametrică sau trei funcții separate care definesc coordonatele în formă parametrică);
- x1 - limita inferioară a variabilei x;
- x2 - limita superioară a variabilei x;
- y1 - limita inferioară a variabilei y;
- y2 - limita superioară a variabilei y;
- xgrid - numărul punctelor de variabila x;
- ygrid - numărul de puncte de variabila y.
Într-un sistem de coordonate, puteți construi unele suprafețe, este suficient pentru a le identifica și apoi programa un șablon pentru a introduce numele lor, fără argumente, separate prin virgulă:
Construcția același grafic în cartezian, cilindrice
și sisteme de coordonate sferice
Să se dea o anumită funcție, cum ar fi z (x, y) = const. Diferitele sisteme de coordonate, această funcție are diferite programe. Într-un sistem de coordonate cartezian este un plan paralel cu planul xy într-o formă cilindrică - un cilindru circular drept cu o rază de bază const, o formă sferică - bilă de Const rază. Pentru a schimba sistemul de coordonate, este necesar să se modelul graficului, faceți clic dreapta în lista care apare, selectați „Properties“, apoi „Date QuickPlot“ și specificați sistemul de coordonate dorit. exemplu:
Pentru construirea de poliedre în Mathcad au funcția de poliedru. Acesta poate fi utilizat în două moduri:
1) numele, atunci apelul funcției ar poliedru ( „numele polyhedron“);
2) codul, atunci apelul funcției ar poliedru ( „număr # poliedru“).
Construcția de suprafețe de revoluție.
Pentru construcția suprafețelor de revoluție în funcție utilă Mathcad CreateMesh.
CreateMesh parametrii funcției:
- x1, y1, z1 - valori ale matricei pentru fiecare coordonată;
- -5 - limita inferioară a variabilei u;
- 5 - limita superioară a variabilei u;
- 0 - limita inferioară a variabilei v;
- 2p - limita superioară a variabilei v;
- 30 - numărul de linii din graficul grilă.
Ecuațiile parametrice pentru rotirea în jurul axei x:
ecuații parametrice pentru cotitură în jurul axei Oy:
Exemplu: Să considerăm o hiperbolă y 2 - x 2 = 1. Când această rotire în jurul hiperboloidul obținut axa Ox hiperbolă a unei coli, prin rotirea în jurul axei Oy - hiperboloid două sub formă de foi. Noi construim suprafața de revoluție:
Construirea unei linii spațiale.
Linie în spațiu, considerat ca locul punctului în mișcare, sistemul apare trei ecuații: x = x (t); y = y (t); z = z (t), exprimă coordonatele punctului t. Aceste ecuații sunt numite ecuațiile parametrice ale liniilor spațiale. Pentru a construi spațiul de linii în Mathcad există o CreateSpace funcție.
- F - parametric vectorul de coordonate ecuații;
- t1 - limita inferioară a variabilei;
- t2 - limita superioară a variabilei;
- tgrid - numărul de linii de grilă; parametru opțional; cu cât valoarea, se obține mai lin linia; în cazul în care nu este suficient de mare, linia se transformă înnodat.
Maple. Construcția de suprafețe și linii spațiale.
Suprafața Program dat funcție explicită.
pot fi trase folosind comanda plot3d (f (x, y), x = x1 ... x2, y = y1 ... y2, opțiuni). Parametrii acestei comenzi se suprapun cu parametrii de comandă complot. Parametrii utilizați frecvent includ comenzi plot3d lumină = [angl1, angl2, c1, c2, c3] - sarcină suprafață iluminat generată dintr-o sursă de lumină punct cu coordonate sferice (angl1 angl2.). Culoarea roșie este definită de lobi (c1), verde (c2) și albastru (c3) de culori care sunt în intervalul [0,1]. seturi de parametri de stil style = opt desen: -points punct, o linie - linie, ASCUNS - angrena cu eliminarea liniilor ascunse, PATCH - umplere (implicit), wireframe - angrena cu ieșire de linii ascunse, CONTUR - linie de nivel, PATCHCONTOUR - umplere și linie de nivel. Parametrul umbrire = opt stabilește o funcție de intensitatea totală, valoarea sa este xyz - implicit, nici unul - fără colorat.
Priver: construi o suprafață x 2 + 4z = 4. Deoarece prima putere a lui z, este posibil să se exprime și să facă funcții explicit, obținem, z =. Vvodimv Maple:
cu (parcele). plot3d (<+ 0. y 2>, x = -5..5, y = -5..5, grid = [25,25], axele = NORMAL)
suprafata Program definita implicit.
Parcela de suprafață tridimensională, având în vedere în mod implicit prin ecuația
, este construit cu ajutorul pachetului de comandă complot: implicitplot3d (F (x, y, z) = c, x = x1..x2, y = y1..y2, z = z1..z2), care specifică ecuația de suprafață
și dimensiunea configurației axelor de coordonate.
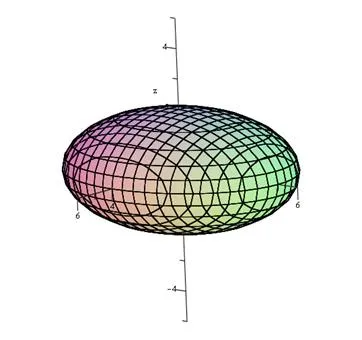
Evident, funcția este dată implicit, deci vom folosi algoritmul descris mai sus.
Suprafața definită parametric Program.
Dacă este necesar pentru a construi suprafață definită parametric: x = x (u, v), y = y (u, v), z = z (u, v), atunci aceste funcții sunt listate în paranteze la echipă: plot3d ([x ( u, v), y (u, v), z (u, v)], u = u1..u2, v = v1..v2).
Exemplu: construi suprafață este specificată parametrically: x = 2. u + v, y = v. cos (u),
z = v. sin (u). Pentru a începe, vom defini funcțiile X0, Y0, Z0, corespunzătoare funcțiilor x, y, z.