compoziţie algoritmică

Teoria haosului a fost dezvoltat de către matematicianul francez Anri Puankare în secolul al XX-lea. Teoria haosului - un aparat matematic care descrie comportamentul anumitor sisteme dinamice neliniare, sub rezerva anumitor condiții, atunci când un fenomen cunoscut sub numele de haos. Comportamentul unui astfel de sistem pare să fie aleatoare, chiar dacă modelul descrie sistemul este determinist. Pentru a sublinia caracterul special studiat în cadrul acestei teorii a fenomenului în mod obișnuit acceptat să folosească numele teoriei haosului dinamic.

Exemple de astfel de sisteme includ atmosfera, turbulență, unele tipuri de aritmii cardiace, populațiile biologice, societatea.

Un bun exemplu al unui sistem dinamic - un pendul simplu. mișcarea sa este definită de doar două variabile: poziția și viteza. Astfel, starea sa - acesta este punctul pe planul al cărui coordonate - poziția pendulului și viteza acestuia. regulă stare Evoluția descrisă, care derivă din legea lui Newton și este exprimată matematic ca o ecuație diferențială. În cazul în care pendulul oscilează înainte și înapoi, starea sa, punctul de pe deplasează avionul de-a lungul unui traseu ( „orbita“). In cazul ideal, fără frecare orbita pendulului este o buclă, cu spirale de frecare orbita la un punct corespunzător pentru a opri pendulului.

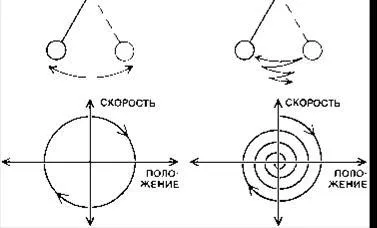
pendulul ca un sistem dinamic, cu o orbită

Sistemele Chaotic sunt împărțite în disipativ (starea de echilibru, are loc într-un mediu de disipare neechilibru furnizat (dispersie) de energie, care este alimentat din exterior) și conservate (conservarea energiei). În natură, cele mai frecvente sisteme disipative.

Din moment ce astfel de sisteme își pierd în mod constant de energie, iar spațiul lor de fază, adică zonă spațială, unde un sistem - este transformat într-o anumită stare numită atractorul sistemului. Atractorii - o structură geometrică, ce caracterizează comportamentul sistemului în spațiul fazelor, după o lungă perioadă de timp. Aproximativ vorbind, un atractor - este ceva ce sistemul tinde să vină la ceea ce ea este atras. Atractor poate fi un singur punct sau un set de puncte. Pentru un sistem haotic aplică cunoscut „efect de fluture“, descris de Edward Lorenz. Orice schimbare mică în valorile inițiale ale variabilelor sistemului este o secvență complet diferită de valori de ieșire.

Apoi, uita-te la principalele tipuri de sisteme haotice și să încerce să facă o cartografiere a simulat, prin utilizarea ecuațiilor neliniare de valori numerice în spațiul de evenimente muzicale.

Ecuațiile matematice care descriu comportamentul sistemelor haotice paradoxal simplu - acestea sunt cunoscute ca ecuații neliniare, adică, având un număr infinit de soluții.

Unidimensională sisteme haotice

ecuația logistică a fost introdus pentru prima dată de sociologul belgian și matematician Pierre Francois Verhulst în 1845 pentru a simula creșterea populației:

Un parametru cheie în această ecuație este - el definește comportamentul sistemului pe termen lung. Valorile de ieșire ecuație logistică depinde de valoarea - mai mică de 3, sistemul este stabilizat la aceeași valoare. Odată cu creșterea - cele două valori, și așa mai departe până la atingerea valorii critice a 3.569946, atunci când sistemul devine imprevizibil. În același mod, luând spațiul de două octave de evenimente muzicale, putem atribui valorile de ieșire ale anumitor note. De exemplu, luând o = 3.3, constatăm că sistemul oscilează între 0,48 și 0,82, care este egală cu repetarea a două note, luând patru - obținem mișcare haotică imprevizibilă a sistemului între 0 și 1, care este mult mai potrivită pentru prepararea Tonuri.

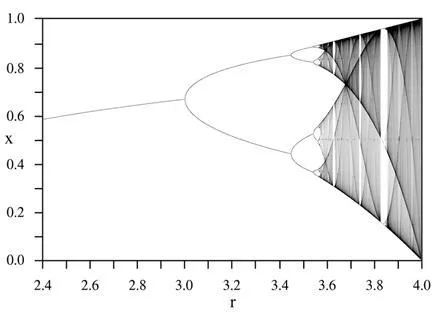
Diagrama bifurcare. Fiecare sector atractor verticală prezintă o anumită valoare. Diagrama arată dublarea perioadei în care crește, care produce în cele din urmă haos

Două-dimensionale sisteme haotice

Henon a fost numit după descoperitorul lui Michel Henon, astronomul francez. Acest atractor nu descrie nici un fenomen natural și a fost creat ca un model bidimensional pentru sistemele haotice disipative. Este exprimată prin următoarele ecuații:

Pentru cartografiere bidimensionale parametru atractori spațiu în evenimente muzicale oferite următoarea secvență de acțiuni. Din moment ce fiecare iterație dă o nouă valoare pentru, alegerea este fie de a atribui parametri muzicale diferite ale acestor variabile, cum ar fi muzica și durate, sau într-o combinație de două variabile, o valoare - distanta de la coordonatele inițiale ale punctului curent pe atractor cu formula:

După ce a primit o secvență lungă de valori, putem calcula frecvența de apariție a anumitor note și se bazează pe faptul că face o melodie. Demn de remarcat faptul că distribuția scorului pentru cartografierea bidimensionale parametri atractori dă distribuția, este similar cu un Gauss.

atractori stranii

În plus față de aceste atractori regulate există atractori stranii. Ciudatul atractor - acest atractor având două diferențe majore de la un atractor convențional: atractor traiectorie astfel nonperiodic (nu este închis) și modul de operare este instabilă (mici abateri de la modul de preluare). Principalul criteriu de atractor haotic este creșterea exponențială a perturbatii mici de timp. Consecința acestui fapt este „amestecarea“ a sistemului este aperiodice în timp oricare sistem de coordonate, un spectru de putere continuă și scăderea funcției de autocorelare timp.

Astfel atractor este Lorenz atractant descris trei ecuații, și în consecință sunt tridimensionale: