Caracteristici ale mișcării de rotație unghiulară a legii de mișcare, viteza unghiulară și accelerație
Caracteristicile mișcării de rotație:
- legea de mișcare unghiulară
- viteza unghiulară este o mărime vectorială care caracterizează viteza de rotație a unui corp rigid, definit ca incrementul unghiului de rotație a corpului într-un interval de timp.
Luați în considerare intervalul de timp infinitezimal → 0. solid At pentru care este rotit cu un unghi infinit de mic Δα jurul axei instantanee uj
Limita la care se urmărește raportul Δα / At. Se numește viteza unghiulară a corpului rigid în momentul în discuție
Viteza unghiulară este o mărime vectorială. Vector viteza unghiulară ω poate fi aplicată la orice punct al axei instantanee și este îndreptată la fiecare moment de timp pe o axă Ω. astfel încât, așteaptă cu nerăbdare acest vector, a se vedea rotația corpului are loc în sens antiorar.
Viteza unghiulară de rotație a corpului - o cantitate vector. .
accelerația angulară este o mărime vectorială egală cu prima derivată a vitezei unghiulare în raport cu timpul:
Când corpul se rotește în jurul unui vector de accelerație unghiulară axă fixă este direcționată de-a lungul axei de rotație în direcția vitezei unghiulare vectorului incremente elementare. vector de mișcare accelerată
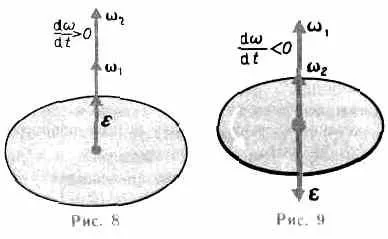
◆ același vector de direcție (Figura 8), când zamedlennom.- direcții opuse (fig. 9).
Caracteristicile de comunicare unghiulare și liniare
Componenta tangențială a accelerației
Componenta normală a accelerației
Astfel, legătura dintre linie și valorile unghiulare (unghiul de rotație , viteza unghiulară (aproximativ accelerația unghiulară (lungimea căii s, punct de-a lungul arcului de cerc cu raza R, liniar viteza v, a accelerația tangențială, accelerația normală AN traversată)) exprimat următoarele formule:
În cazul punctelor de mișcare uniform accelerată de-a lungul unui cerc ( = const)
Momentul de inerție - o mărime fizică scalară. o măsură a inerției în mișcarea de rotație în jurul axei. Caracterizat prin distribuția masei în organism: momentul de inerție egală cu suma produselor masei elementare cu pătratul distanței lor față de setul de bază (punct, linie sau plane).
Momentul cinetic al unui punct în raport de material într-un punct de referință determinat de produsul vectorial al razei vectorului său impuls și:
în care: - raza-vector în raport cu particulele selectate în punctul de referință al sistemului de referință fix, - impulsul particulei.
Pentru mai multe moment, un impuls de particule este definit ca (vector) suma acestor membri:
în care - vectorul rază și impulsul fiecărei particule incluse în sistem, timpul care este determinată de pulsul.
(În limita numărului de particule pot fi fără sfârșit, de exemplu, în cazul unui corp solid, cu o masă distribuită în mod continuu sau chiar un sistem distribuit, acest lucru poate fi scris ca în cazul în care - pulsul unui element infinitezimal al unui sistem de puncte).
În sistemul SI momentul cinetic se măsoară în unități de jouli -sekunda; J · s.
Din definiția momentului unghiular aditivitate sale. ca și pentru sistemele de particule, în special, și pentru un sistem format din mai multe subsisteme executate:
.