Capitolul 2 moment de forță în raport cu centrul

§6. Momentul de forță în jurul centrului (sau punct)

Atunci când se analizează sistemul spațial al forțelor aplicate conceptului de momentul forței în raport cu centrul (sau punct).

Definiția. moment de forță

despre centrul G este atașat centrului despre vector, modulul este egal cu produsul dintre modulul de alimentare F pe oră ei umăr și care este orientat perpendicular pe planul ce trece prin centrul O și forța în direcția din care forța care tinde să transforme corpul vizibil in jurul centrului O anti-orar (fig. 17). forța F Umăr h din centrul G se numește lungimea segmentului perpendicular scăzut de la punctul O la linia de acțiune a forței.

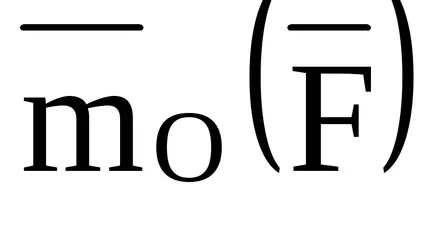
Conform acestei definiții

cuplul măsurat în Newton-metri (Nm).

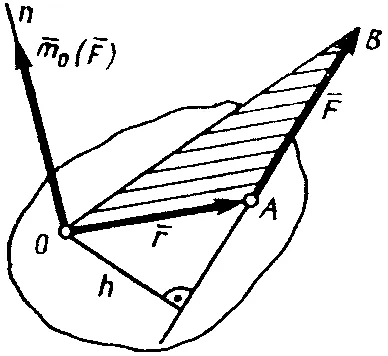
Pentru a găsi formula care exprimă vectorul

, ia în considerare produsul vectorial. prin definiție,

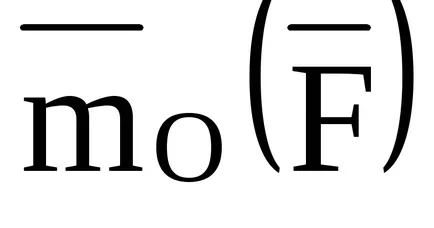
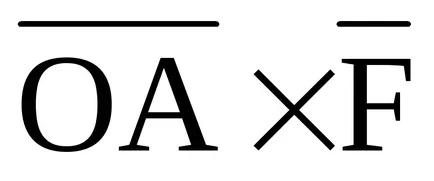
vector dirijat

perpendicular pe planul OAB în direcția din care cea mai scurta combinatiecu(În cazul în care sunt puse în afara de un singur punct) poate fi văzut loc anti-sensul acelor de ceasornic, adică, precum vectorul. În consecință, vectoriișiexprimă aceeași sumă. aici

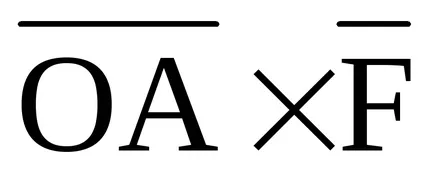
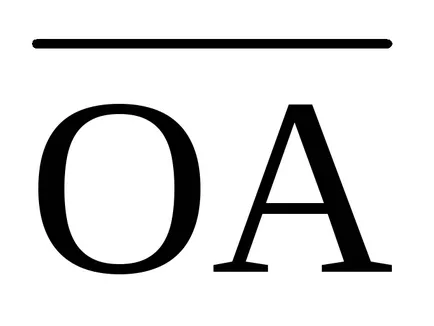
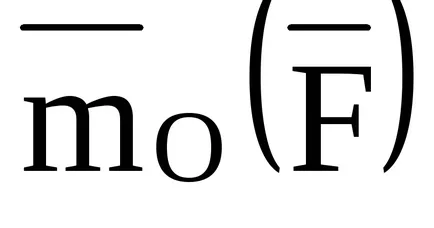
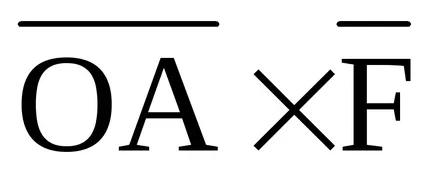
unde

- vectorul raza punctului A, trase din centrul O.

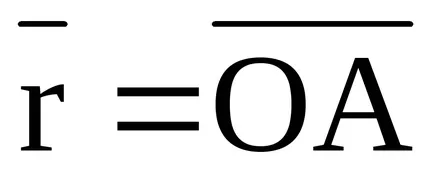
moment de forță

Acesta are următoarele proprietăți:

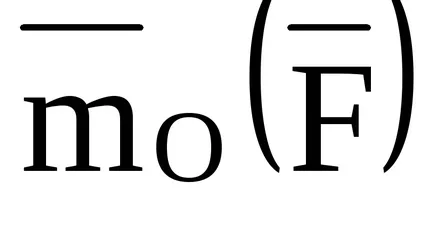
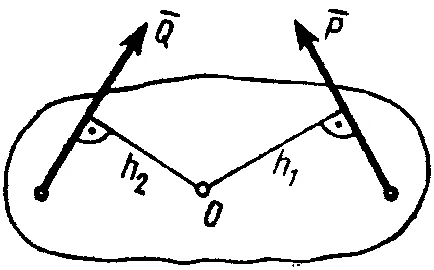
1) în momentul de forță în jurul centrului nu se schimbă atunci când se deplasează punctul de aplicare a forței de-a lungul liniei sale de acțiune;

2) momentul forței în jurul centrului O este zero sau când puterea este zero, sau atunci când linia de acțiune a forței trece prin centrul O (brațul este zero).

§7. momentul algebrică de forță în raport cu centrul

Atunci când se analizează sistemul de plat al forțelor folosit conceptul de momentul algebrice de forță în raport cu centrul. Atunci când toate sistemele de alimentare se află într-un singur plan, momentele lor despre orice centru O situată pe același plan, perpendicular pe acest plan, adică direcționat de-a lungul aceleiași linii. Apoi, fără a recurge la direcția vectorului simbolism al acestor momente poate fi unul distinge de celălalt semn și ia în considerare momentul de forță

în raport cu centrul O ca valoare algebrică. Suntem de acord cu un timp numit algebrică și reprezintă. momentul algebrică de forțădespre centrul O ravenvzyatomu cu produsul modul semn corespunzător al forței pe umăr, și anume,

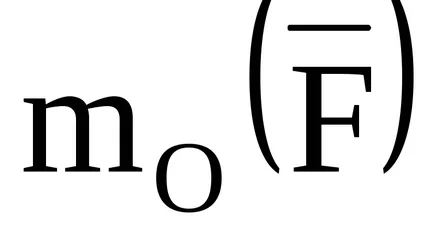
În același timp, este considerat pozitiv atunci când forța tinde să se transforme corpul în jurul centrului O anti-sensul acelor de ceasornic, și negativ - atunci când sensul acelor de ceasornic. Atât de mult pentru puterea arătată în fig. 18:

,.

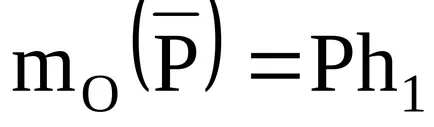
§8. O pereche de forțe. moment de cuplu

O pereche de forțe este un sistem de două egale în mărime, paralele și orientate opus forțelor care acționează asupra unui corp rigid (Fig. 19a).

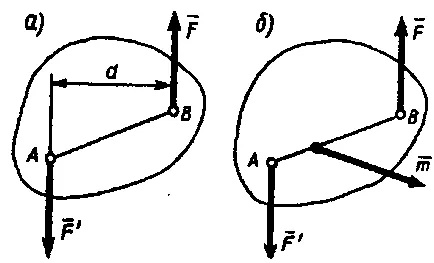
sistemul de alimentare

,, formând o pereche nu este în echilibru (aceste forțe sunt dirijate de-a lungul unei singure linii (axioma 1)). În același timp, cuplul nu are nici un rezultat, deoarece. Prin urmare, proprietățile unei perechi de forțe ca un nou membru independent al staticii, ar trebui să fie luate în considerare separat.

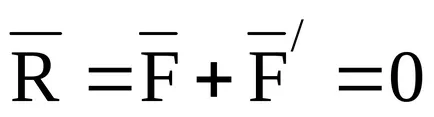
Planul care trece prin linia de acțiune a forței de perechi, numit planul cuplului. Distanța d dintre liniile forțelor numite cuplu de perechi de umăr. Acțiunea unei perechi de forțe pe un corp rigid este redus la un anumit moment de rotație a cuplului.

Definiție: Un moment al unei perechi de forțe este un vector

, modulul este egal cu produsul dintre modulul de unul dintr-o pereche de forțe de pe umărul său și care este orientată perpendicular pe planul pereche de pași în direcția din care o pereche de corp vizibil tinde să se rotească în sens antiorar (fig. 19b), adică

.

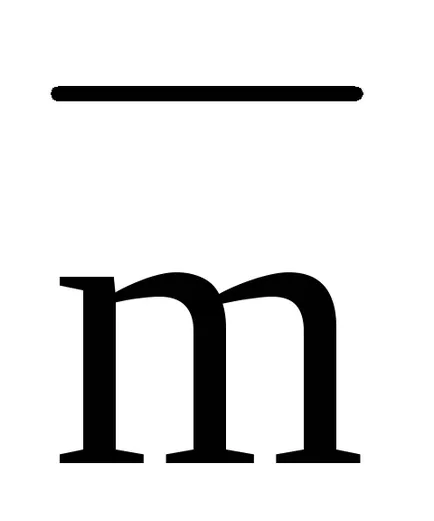
In contrast, momentul pereche vector forță este liber de vector, adică, acesta poate fi transferat la orice punct al corpului.

Perechea de timp poate da o altă expresie: în momentul în care perechea este egală cu suma momentelor în ceea ce privește orice centru O, formând o pereche de forțe, și anume,

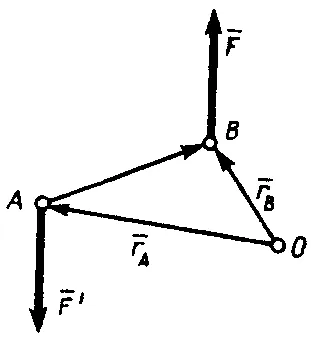
Pentru a dovedi comportamentul unui punct arbitrar O (fig. 20), vectorul de poziție

și. Apoi, în conformitate cu formula (12), luând în considerare, de asemenea, că, obținem

,

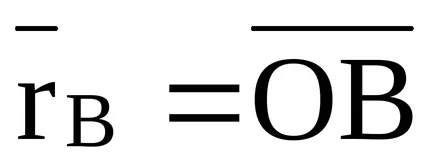
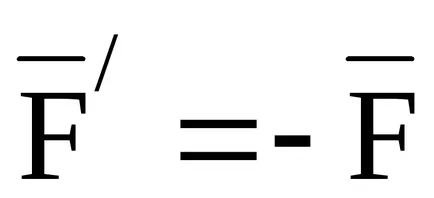
deoarece

, egalitatea (14) este demonstrată. Prin urmare, în special, deja menționat mai sus rezultat

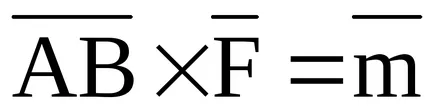
și anume perechi În prezent egale cu forțele moment de una din punctul său relativ de aplicare a forței. altă Rețineți, de asemenea, că în momentul în care perechile de module

Din (14) rezultă că cele două perechi de forțe care au aceleași puncte sunt echivalente.

Din (14) rezultă că în continuare în cazul în care organismul acționează asupra câteva momente perechi

,, ..., suma momentelor tuturor forțelor care alcătuiesc perechi, cu privire la orice centru va fi egal, și în consecință, întregul set de aceste perechi este echivalentă cu o singură pereche de un punct

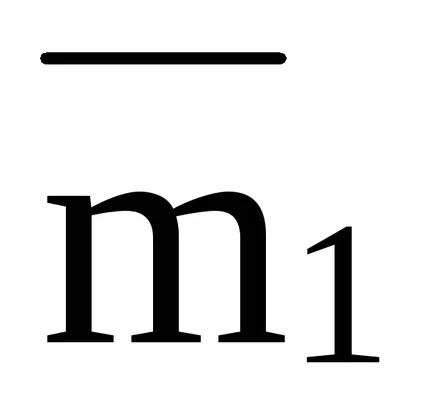
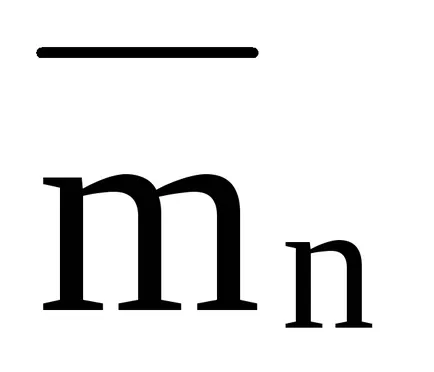
Acest rezultat exprimă teorema adăugarea de abur.