câmp de viteze Vector
Într-un mediu fix ca întreg, viteza medie a moleculelor din dV volum va fi egal cu zero. Într-un flux de mișcare este valoarea medie a v nu mai este zero. Noi numim această rată fluxul de viteză într-un punct dat în spațiu (care este elementul de volum dV), la un moment dat v = v (x, y, z, t) = v (r, t). Această caracteristică oferă un nou obiect matematic - câmpul vectorial de viteză.
În viitor, un interes mai mare pentru noi va fi un alt câmp vectorial asociat cu pulsul mediului. Puls volum dV va fi egal cu: dp = DMV, împărțirea de volumul dV obține volumul pulsului unității în mișcare medie. Vom numi această cantitate pe unitatea de volum a densității de impuls a impulsului mediu sau:
.
La volumul ris.21.1 limitează suprafața închisă S. se împarte în porțiuni mici dS. Cu fiecare dintre ele, putem asocia o zonă elementar vector, după cum urmează:
unde vectorul n - versorul lungul normal dS site.
dm substanță Mass transferabile prin sol pe unitatea de timp (agent de curgere) va fi egal cu produsul scalar al vectorului Ds densitate puls:
Fluxul de material prin suprafața S închisă (masa de substanță transferată pe prin ea unitatea de timp) este egală cu integrala pe suprafata:
Cercul simbol în centrul semnului integralei înseamnă integrarea pe o suprafață închisă. In (22.1) și (22.2) greutate dm- magnitudine de ordin superior în raport cu dm masa s. Dacă o variabilă m s implică masa materiei delimitată de suprafața S închisă, atunci ecuația (2.22) va fi un semn minus. Derivatul totală Timpul înlocuiți derivata parțială, presupunând că volumul delimitat de suprafața închisă S. staționare:
.
Cu orice câmp vectorial putem lega o divergență câmp scalar. Divergenta (din latină di-verto - divergente) câmpul vectorial (pv) la un anumit punct în spațiu este determinat ca raport de curgere vectorul limită (pv) printr-o suprafață închisă la volumul acesta limitat (punct de interes este în acest volum, se micșorează cu o scădere în acest punct):
O valoare pozitivă de divergență la un anumit punct al unui flux staționar ne spune că aceasta este sursa substanței, aceasta este sursa. De exemplu, în fluxul de râu poate fi puncte de pe albia râului, în cazul în care a lovit cheile din surse subterane. La aceste puncte, divergența câmpului vectorial (p v) pozitiv. Dacă râul omis tubul prin care face retrageri, punctul de pe conducta de tăiere poate fi în continuare inclusă în câmpul vectorial al debitului râului (curgere în conductă sunt considerate separat), divergența va fi negativ.
În sursele de flux și chiuvete fără diferență de la zero în niciun rezultat punctul div (p v) într-o schimbare cu densitate de timp:
Definim divergența unui vector arbitrar Un câmp într-un sistem de coordonate cartezian.
Să presupunem că punctul definit de un vector rază r vectorul A este direcționat astfel încât să fie cu axele sistemului de coordonate unghiuri mai mici Pi / 2 (ris.22.1). Pune punctul în centrul cubului cu margini dx, dy, dz. pad elementar dS1i DS2 axe perpendiculare Ox (Ox OS1parallelen axa vector și vectorul este antiparalel OS2- s). Apoi fluxul de vector A prin dS1polozhitelen pad și prin negativ dS2- pad (același rezultat se obține pentru axele y și z):
.
Am obținut o expresie pentru divergența câmpului vectorial în coordonate carteziene, care pot fi scrise folosind operatorul Hamiltonian sub forma produsului scalar:
Dacă volumul V, delimitat de o suprafață închisă S. împărțit în două părți, prima este delimitată de o suprafață închisă Deci + S1, al doilea - Deci + S2, atunci
.
Se poate observa că debitul prin suprafața S închisă este egală cu suma fluxurilor prin volumele delimitatori de suprafață închise pentru care am împărțit V. Volumul Același rezultat se obține prin împărțirea volumului într-o multitudine de mici cantități contigue DVI:
.
Folosind acest rezultat și definirea divergenței putem dovedi teorema lui Gauss:
.
După limita ca aspirație pentru a obține DVI dreptul la zero ecuația integrală va fi corecte:
Astfel, vectorul flux A prin suprafața S închisă este egală cu integrala divergența volumului calculat vectorul A. V. care limitează suprafața închisă S. Relația (6.22) este teorema lui Gauss, este valabil pentru orice câmp vectorial.
Atunci când se deplasează suportul solid pentru vizualizarea câmpului vectorial vitezei de utilizare noțiunea de linie flux - o linie tangentă la care fiecare punct coincide cu direcția vitezei de curgere în acest punct. În calea de mișcare constantă a oricărei particule în fluxul se potrivește cu linia curentă. O pluralitate de trecere printr-o curbă închisă a forma un curent de flux tub. Într-un flux constant lent de particule care se deplasează în tubul de curgere, fără a se îndepărta de la domeniul său de aplicare, o astfel de curgere nu se agită numite straturi laminare (din lamina Latină - placă). Prin creșterea debitului sau a fluxului de obstacole posibile pierderea stabilității curgerii, mișcarea particulelor de dimensiune medie este mai puțin ordonată, în cazul limită, haotic (picătură de apă scade după mișcare). In mai putin ordonat, dar nu complet aleatoare de mișcare, ceea ce se numește o turbulent, putem evidenția mișcarea turbionară a particulelor. În fotografie puteți vedea vârtejurile (dintre care unele sunt indicate prin săgeți), care au fost formate după fluxul de sprijin Neva Palace Bridge.
Pentru a descrie o astfel de mișcare turbionară, introducem conceptul de circulație a vectorului v într-un circuit închis L:
Pe fotografie arată calea de curgere pentru circulație L., care nu este zero.
Notă aditivitate circulație: circulație a conturului L (ris.22.2a)
va fi egală cu suma circulă prin L1 și L2, deoarece integrala de pe site-ul ab vom calcula de două ori, merge în direcția opusă.
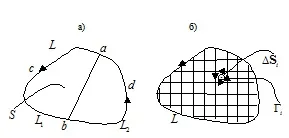
Dacă rupt contur într-o multitudine de bucle mici (ris.22.2b), apoi
.
După determinarea rotorului de circulație a defini un nou câmp vectorial v (r t) (de rotație latină - sens giratoriu). În vecinătatea fiecărui punct al fluxului de o buclă închisă, descoperim circulația viteza v pe aceasta, împărțită la zona delimitată de conturul. Am găsit limita raportului
care ne va da valoarea proiecției noului rotv vectorului în direcția Ds vectoriale. La calcularea direcției de circulare a circuitului de bypass sunt alese astfel încât după cum se arată în ris.22.3a. În același DS-> 0, astfel încât bucla este contractat la un punct, rotv în care dorim să determinăm.
Pentru a găsi proiecții rotv ale vectorului într-un sistem de coordonate cartezian, trebuie să facem o operație similară pentru cele trei site-uri DSX, DSY, DSZ (ris.22.3b). În special, pentru a se obține proiecția x (ris.22.3v) axe:
Vectorul de ardere preferat rotv folosind produsul determinant sau vector folosind operatorul Hamiltonian:
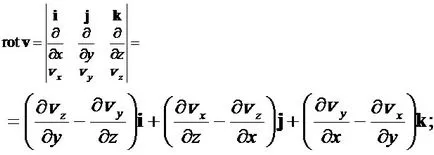
Folosind definiția circulației și aditivitatea ei putem fi demonstrată pentru un câmp vectorial arbitrar Stokes teorema:
.
După trecerea la limita prevăzută DSi-> obține suprafața dreapta integrală, și egalitatea ar fi corecte:
Astfel, vectorul A circulație într-un circuit închis L este vectorul flux rota prin suprafața S închisă, delimitată de conturul L. Ecuația (22.9) - Stokes teorema, este valabilă pentru orice câmp vectorial.
Orice câmp vectorial arbitrar A, putem reprezenta suma a două domenii - potențialul A1, egal cu gradientul unui câmp scalar, iar A2 vortex: A = A1 + A2. Pentru prima condiție rotA1 = 0 la fiecare punct în spațiu, pentru al doilea - divA2 = 0. Câmpul vectorial în viteza de curgere a apei în Neve arătat în fotografiile pot fi, de asemenea, reprezentat ca o sumă a două câmpuri. Primul câmp își poate asuma potențialul v1, dacă vom neglija frecarea internă în apă, un al doilea v2 câmp va fi relevant pentru vârtejuri în fluxul.