Bogdanov la

§ 6.RAVNOMERNOE mișcare circulară: accelerația centripetă.

Viteza Vector a unui corp în mișcare circumferențial continuu își schimbă direcția, și, prin urmare, o astfel de circulație este accelerată.

Orice mișcare de-a lungul unei curbe de accelerare cale se produce, deoarece vectorul viteză dirijat tangențial traiectoria își schimbă direcția cu timpul. Exemple de mișcare curbilinie poate fi mișcarea planetelor în jurul Soarelui și electronii din jurul nucleului. De-a lungul unui traseu curbat masina se misca, de cotitură într-o intersecție, iar aeronava apel la aterizare.

Cea mai simplă este mișcarea curbilinie mișcare circulară uniformă. în care modulul vitezei rămâne constantă, dar direcția se schimbă. Pentru a găsi mărimea și direcția vectorului accelerație la uniformă pe un punct central al cercului O. mișcarea notă pe acestea două puncte strâns distanțate între ele A și B (a se vedea. Partea superioară a Fig. 6, stânga). Să punctul Un corp a fost în timpul t. iar la punctul B - la momentul t + D t. În aceeași figură care iese din punctele A și B sunt trase vectori vA și vB. Vitezele corporale corespunzătoare punctelor de date.

Accelerații. sunt cunoscute (a se vedea. § 4), este egal cu raportul dintre rata de schimbare a vectorului D v. a avut loc în timpul intervalului de timp D t. la valoarea intervalului, din care rezultă că D v = a. D t. În cazul nostru, D v = vA - vB. Chiar în partea de sus din Figura 6 arată cum, folosind regula triunghi, găsiți cunoscut D v și vB vA. Când se apropie punctele B și C și direcția se apropie pe direcția perpendiculară. și astfel devine o direcție spre centrul cercului de-a lungul căruia corpul se mișcă. O astfel de mișcare este numită mișcare cu accelerația centripetă.

Deoarece și vB sunt vA perpendiculare OA și OB. respectiv, precum și modulele vA și vB sunt egale, atunci triunghiul OAB și O'A'B „sunt similare ca triunghiuri isoscele cu unghiuri egale (a se vedea. Figura 6 sus). Prin urmare, următoarea relație între lungimile laturilor triunghiului:

Pentru punctele strâns distanțate A și B de lungime AB poate fi considerată egală cu lungimea corespunzătoare circumferința arcului AB și lungimea arcului circumferinței egală cu produsul dintre modulul vitezei, v la D t. Substituind (6.1) A'b „= a. D t, AB = v. D t. O'A „= v. OA = R (raza cercului), obținem după transformări simple, următoarea expresie pentru amplitudinea accelerației centripete:

Orice mișcare curbilinie peste traseu distanțe scurte pot fi întotdeauna considerate ca mișcarea unui arc de cerc cu o rază mică cea mai potrivită pentru o anumită porțiune a căii (vezi. R1. R2 și R3, în partea de jos din figura 6). Acest interval se numește raza de curbură a traiectoriei sale în acest punct. În cazul în care corpul se mișcă uniform (modulul de viteză, v nu este schimbat) de-a lungul unui traseu curbat, apoi cu 6,2 și cunoscute razele de curbură este posibilă calcularea accelerației centripete îndreptate spre centrul curbei căii în orice punct.

Deoarece accelerația centripetă este întotdeauna direcționată perpendicular pe tangenta la traiectoria, direcția vectorului accelerație în mișcare curbiliniu nu coincide întotdeauna cu direcția tangentei cale. Prin urmare, vectorul accelerație în acest caz reprezintă suma celor două componente perpendiculare reciproc: tangențiale, AT (tangențial la traiectoria) și normală, AS (direcționat perpendicular pe tangenta). În acest caz, modulul AT corespunde unei modificări a vitezei de deplasare, iar An - schimba direcția vectorului său.

Examinați Întrebări:

· În cazul în care accelerația centripetă este direcționată, și modul în care aceasta depinde de viteza și raza cercului?

· Care sunt modulele tangențiale de accelerare și normală în mișcare uniformă într-un cerc?

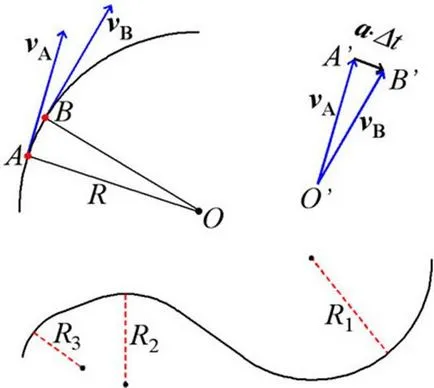
Fig. 6. Top - conchide formulă pentru accelerația centripetă; de jos - un traseu curbat, unele secțiuni ale care pot fi înlocuite cu arce circulare rază desemnate.