bandă Mobius, platforma de conținut

Chernova Anna Nikolaevna

Obiectiv: Fiecare dintre noi are o idee intuitivă a ceea ce „suprafață“. Suprafața foii de hârtie, suprafața peretelui de clasă suprafața globului sunt cunoscute tuturor. Ar putea fi faptul că - ceva neașteptat și chiar misterios într-un astfel de concept convențional? bandă EXEMPLU Mobius indică faptul că se poate.

1. Care este banda Mobius?

2.Veliky matematician - astronom.

4. Cum sa faci o bandă Mobius.

5. Câte părți are o bandă Mobius?

6. Soldatik- Changeling.

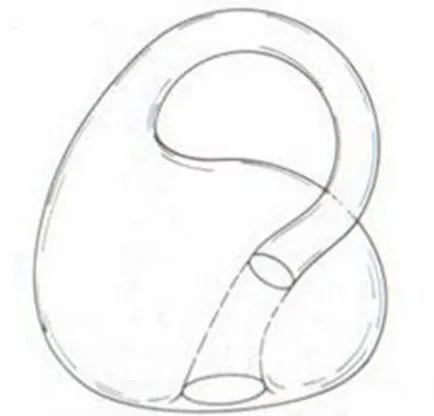
Care este banda Mobius?

Topologia este nevoie de matematicieni aproape toate specialitățile, este foarte frumos, metoda ei în comparație cu alte oferi simultan teoreme mai larg, mai puternice și mai simple.

Banda Möbius este foarte ușor de făcut, ține în mâinile lor, să taie, să experimenteze ca orice altceva. Studiu Möbius benzi - o bună introducere la elementele topologiei: teorema lui Euler, colorat, versatilitatea, noțiunea de mapări continue.

Închide obiect geometric „ciudat“ este sticla Klein. Klein sticla poate fi obținută prin legarea a două benzi Mobius la margini. Într-un spațiu euclidian tridimensional convențional pentru a face acest lucru fără a crea auto-intersecții, este imposibil.

Alte scoruri similare - planul proiectiv reale. În cazul în care gaura puncție în planul proiectivă reale, atunci ceea ce a mai rămas este o bandă Möbius. Pe de altă parte, dacă lipi discul la o bandă Möbius, combinând limitele lor, rezultatul este planul proiectiv. Pentru a vizualiza acest lucru, este util să se deformeze banda Möbius, astfel încât marginea sa a devenit un cerc comun. O astfel de formă se numește „cap dur“ (acoperire dur poate însemna, de asemenea, aceeași formă cu discul încleiat, adică imersiune planul proiectiv în R3).

Există o concepție greșită comună că capacul dur nu poate fi format în trei dimensiuni, fără suprafață de auto-se intersectează. De fapt, este posibil pentru a pune o bandă Möbius în R3 cu limita, care este un cerc perfect. Ideea este după cum urmează: - Fie C cercul unitate în planul xy în R 3. Combinarea punctului antipozi în C. adică punctul în unghiuri # 952; și # 952; + Π arc de cerc, obținem că pentru # 952; între 0 și 2 arce / tt situate deasupra planul xy. pentru alții # 952; de mai jos (și în două locuri cu arc electric se află în planul xy).

Se poate observa faptul că dacă discul este atașat la cercul de delimitare, auto-intersecția planului proiectiv rezultat legat în spațiul tridimensional. În ceea ce privește laturile de referință ale pieței, așa cum sa arătat mai sus, planul proiectiv real, se obține prin lipirea „persistență“ orientarea celor două părți rămase.

Cum sa faci o bandă Mobius.

Ia hârtie bandă AVSD împărțit în jumătate de-a lungul lățimii liniei punctate (vezi. Fig.) Se aplică capetele AB și CD reciproc și se lipesc între ele. Dar nu este la fel de oribil, de asemenea, la punctul A coincide cu punctul D, și punctul B - la punctul C. răsucim banda dată înainte de lipire. Sa dovedit celebru în inel de hârtie matematică. Ea are chiar si un nume special - o bandă Mobius. Acum am tăiat banda cu foarfece lipite în mijloc, de-a lungul liniei punctate. Desigur, în cazul în care nu răsucite bandă înainte de lipire totul ar fi simplu: un inel lat am avea două înguste. Și acum ce?

Câte părți are o bandă Mobius?

În banda de la care se face banda Mobius, există două părți. Și el însuși, este doar o parte!

Să încercăm să picteze banda Möbius - bucată cu bucată, fără a trece peste marginea benzii. Și ce sa întâmplat? Ai vopsea peste tot banda Mobius! „Dacă cineva - a trebuit vreodată să picteze“ doar o „suprafață de stronțiu de benzi Mobius, deși este mai bine să-l scufundați într-o galeata de vopsea“ - scrisă de Richard Courant și Herbert Robbins în excelenta sa carte „Ce este matematica.“

În cazul în care interiorul inelului de obicei de plante paianjen, iar pe exterior - pentru a le permite să zboare și să se târască în mod arbitrar interzicerea doar pentru a urca peste marginea inelului, atunci păianjenul nu va fi capabil de a ajunge pentru a acoperi. Și dacă ambele le-a pus pe o bandă Mobius, cei săraci vor fi mâncat o muscă, cu excepția cazului în desigur, păianjenul se taraste mai repede.

Am tăiat un soldat de hârtie și a trimis-o de-a lungul liniei punctate, mersul pe jos în mijlocul unei benzi Mobius. Și el a revenit la punctul de plecare. Dar, în ce formă! În susul în jos! Și așa sa dus înapoi la început în poziția normală, este necesar să se facă o mai „krugolistnoe“ călătorie. Verificați!

Experimentele pentru toată lumea.

Ia banda, împărțiți fiecare parte în trei fâșii egale și lipici, torsiune dată o bandă Mobius. Vom fi tăiat de-a lungul liniei punctate. Dacă banda nu este răsucită, atunci mai întâi ne-ar tăia un inel și apoi două mai multe altele. Toate cele trei inele, fiecare de aceeași lungime ca și originalul, dar mai puțin de trei ori lățimea. Dar avem o bandă Mobius. Și „nu a luat“ foarfece de hârtie, tăiate de-a lungul liniilor punctate dintr-o dată și obține două inele interblocate. Una dintre ele este de două ori, atâta timp cât sursa și răsucite de două ori. În al doilea rând - Möbius benzi, lățimea, care este de trei ori mai mică decât originalul.

CONCLUZIE: Acest lucru poate ajuta pe elevi să se extindă lor

KEN. Învățat în conceptele obișnuite SEARCH neașteptate și chiar misterios.

1.Vneklassnaya lucru în matematică.

3.KRATKY OCHEREK istoria matematicii. DY Struik. traducere

din germană și completările I. B.POGREBYSSKOGO.