Arbori orientate, ordonată și binar

Lemn - un grafic, care se caracterizează prin următoarele proprietăți:

1. Există un element unic (nod sau nod), care nu se referă la orice alt element - și care se numește rădăcină.

2. Începând de la rădăcină și în continuarea unei anumite indicii de lanț conținute în elemente, este posibil accesul la orice element de structură.

Numele de „copac“ vine de la echivalența logică a arborelui abstract structură arborescentă în teoria grafurilor. Legătura de comunicație între o pereche de noduri din ramurile copacilor sunt numite de obicei. Acele noduri care nu se referă la alte noduri din arbore, numit o frunză (sau nodurile terminale) Nodul care nu este o frunză sau rădăcină, acesta este considerat a fi un nod intermediar sau o ramură (sau nod intern neterminal).

Pentru un grafic direcționat numărul muchiilor care provin de la niște vârfuri V inițiale, se numește outdegree acest nod. Numărul de muchii pentru care un nod V este finit, numit indegree vertex V, iar suma outdegree și nodurile de setare V numită măsura de sus.

Următoarele vor fi prezentate la o clasă importantă de grafice - arbori orientate - și terminologia corespunzătoare. Copacii au nevoie pentru a descrie orice structură cu o ierarhie. Exemple tradiționale de astfel de structuri: arbori de familie, clasificarea zecimală a cărților în biblioteci, ierarhia pozițiilor în cadrul organizației, o expresie algebrică care implică operațiuni care sunt prescrise anumite reguli de prioritate.

arbore Oriented - este un astfel de grafic direcționat aciclic (digraph), în care un nod numit rădăcină, are indegree de 0, iar restul - indegree de 1. Un arbore orientat trebuie să aibă cel puțin un nod. Vârful izolat este de asemenea orientată spre copac.

Vertex-based outdegree arborele care este zero, aceasta se numește END (suspensie) sau apex a foii; toate celelalte vârfuri ale arborelui se numește noduri ramură. Lungimea de la rădăcină la un nod numit LEVEL (NUMBER STRAT) din acest vertex. root pe bază de lemn este egal cu zero, iar nivelul oricărui alt nod este distanța (adică diferența în cifre absolute de niveluri vârfuri) între acest vârf și rădăcina. copac Oriented este un grafic aciclic, tot drumul în ea elementar.

În multe aplicații, ordinea relativă a nodurilor din fiecare nivel are o anumită semnificație. Atunci când vizualizarea arbore în care computerul este introdus automat un astfel de ordin, chiar dacă este în sine arbitrar. Secvența de noduri într-un anumit nivel, puteți introduce cu ușurință, marcând un nod ca primul, iar celălalt - ca al doilea, etc. În loc de a comanda nodurile pot specifica ordinea de pe margini. Dacă copac orientat la fiecare nivel este dat ordinul nodurilor, un astfel de copac este un copac ordonat.

De asemenea, vom introduce unele dintre conceptele asociate cu copaci.

Nodul X este numit strămoș (sau tată), și Y și Z sunt numite noduri moștenitor (sau fii) între ele, respectiv, sunt numite frați. Și stânga este fiul fiul cel mare, iar dreapta - cel mai mic. Numărul de subarbori dintr-un anumit vârf se numește gradul de vârfuri. (În acest exemplu, X este 2 subramificație deci GRADUL vertex X este

În cazul în care rădăcina arborelui și îndepărtați nervurile care se conectează rădăcina cu vârfurile primul nivel, veți obține o mulțime de copaci care nu au legătură. Setul este numit un copaci de pădure nelegat

Am văzut că secvențele și listele pot fi definite, pentru a partaja după cum urmează: orice secvență (de spin-suc), cu un tip de bază de T - este fie:

secvență goală (lista); sau

concatenare (lanț) ale elementelor și secvența ratei T Flow cu tipul de bază T.

Aici, pentru principiile de structurare definire (urmeaza studiu sau o iterație) folosind recursivitate. În urma iterație și sunt atât de comune încât acestea sunt, de obicei, se topesc fundamentală schi „imagine“, ca structuri de date și programe „de management“. Cu toate acestea, ar trebui să ne amintim întotdeauna că folosind recursivitatea acestea pot fi definite numai lyat, dar recursie poate fi în mod eficient și elegant utilizează cuva pentru a defini structuri mai complexe.

Un exemplu bine cunoscut este copaci. Să structura vovidnaya-nucleu este definită după cum urmează: core-vovidnaya structura tip de bază cu T - este fie:

1) o structură goală; sau

2) ansamblul de tip T, care este asociat cu un număr finit de structuri arborescente-TION cu tipul de bază T-numit revyami indiscreti.

Din similitudinea definițiilor recursive consecvent structurilor stey si arboricole se poate observa că secvența (lista) este o structură de arbore în care fiecare nod are cel mult un „subarbore“. Prin urmare, adept-ness (lista) este, de asemenea, numit un copac degenerat.

Există diferite moduri de imagine structură arborescentă. De exemplu, să presupunem că tipul de bază T este un set de litere; această structură de arbore în diferite moduri izo-lipirii, în Fig. Toate aceste idei demonstrează aceeași structură, și, prin urmare, echivalent. Cu pomoschyugrafa puteți vizualiza conexiunile de ramificare care au condus la înțeles obscheupotrebitel pe termen termenul „arbore“. Cu toate acestea, destul de ciudat, de copaci a decis să picteze cu susul în jos, sau - în cazul în care se preferă să-și exprime acest lucru în mod diferit - pentru a reprezenta rădăcinile copacului. Dar această din urmă formulare este înșelătoare, deoarece nodul superior (A) este de obicei nazyvayutkornem. Deși mysoznaem că natura copacilor nu-mult mai complexe decât structuri de abstractizare noastre, vom continua structura de copac numit un copac.

copac comandat - un copac care a kazh-Dogo nod ordonat sucursale. În consecință, cele două ordonat-guvernamentală tree- este specială, diferită de alți copaci. Nodul y, care este direct sub nodul x este denumit (direct) x descendent; dacă l este naurovneI, noi spunem chtou - pe urovnei - \ - \. Dimpotrivă, uzelh numit (directe) stramos de la. Se crede că rădăcina copacului este situat la nivelul 1. Maxi-mal nivel de orice element al arborelui se numește adâncimea sau înălțimea acestuia.

Dacă elementul nu are descendenți este numit un membru terminal sau membru foaie și un non-terminal, nodul nazyvaetsyavnutrennim. Număr (Nepo-sredstvenno) descendenții nod intern numit egostepenyu. Gradul maxim de toate nodurile este o putere de-hohote. Numărul de sucursale, sau margini care trebuie să treacă pentru a trece de la rădăcină la uzluh, nazyvaetsyadlinoy cale .Koren are o lungime de cale de 1, descendenții ei imediate - .. 2 lungimea căii, etc. în general, un nod la nivel I are o lungime de cale Lungimea L lemnul este definit ca suma lungimilor pu-dren ale tuturor unităților sale. Este, de asemenea, numit lungimea modul intra-l. De exemplu, lungimea traseului arbore interior, prezentat în fig. 2.1, egală cu 52.

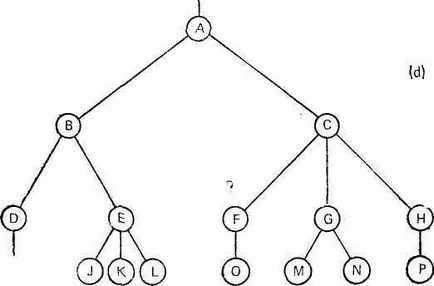
Figura structura arbore 2.1.Predstavleniya.

În scopul de a determina ceea ce se numește lungimea căii extrinsecă, vom completa un nod special de copac de fiecare dată când vstre-chaetsya zero, subramificație. În același timp, credem că toate nodurile trebuie să aibă același grad - gradul de lemn. Track-quently, o astfel de extindere a arborelui presupune umplerea ramurile goale, desigur, unitățile speciale nu au descendenți suplimentare. Arborele prezentat în Fig. 2.1, complement nennoe noduri speciale, prezentate în Fig. 2.3, unde nodurile spe-cial reprezentate prin pătrate.

Fig. 2.2 Două arbore binar diferit.

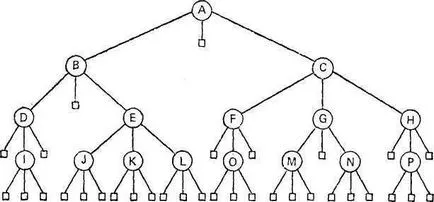
Fig. 2.3. arbore ternar cu noduri speciale.

Lungimea căii extrinsecă este acum definită ca suma dlinputey toate unitățile speciale. Un copac, prezentat în Fig. 2.3, lungimea traseului exterior 153 este egal.

Numărul de noduri speciale m pentru a fi adăugate la pomul grad d, depinde direct de numărul n noduri este-Khodnev. Rețineți că fiecare nod indică exact o ramură. Prin urmare, există o subramificație m -F- n ramuri extinse. Pe de altă parte, de la fiecare nod sursă sucursale d afară și de noduri speciale - audio. In aceasta, toate ramurile imeetsyadn -F- 1 (1 permite ramură, arătând spre rădăcina-conductoare). Din aceste două ecuații, obținem următoarea egalitate actuală m între numărul de componente speciale și n-TION pornire nodului: dn + 1 = m -F- n, sau

Numărul maxim de noduri din arbore predeterminat înălțimea h este realizată în cazul în care toate nodurile au subarbori cu excepția d nivel h, fara noduri. Apoi, gradul d arborele primul nivel 1 cuprinde un nod (root) d level2 conține copii săi, Nivelul 3 conține copii d2 d Tier 2 noduri etc. Aceasta dă următoarea valoare ..:

ca numărul maxim de noduri pentru un arbore cu o înălțime h și un grad d. Pentru d = 2 obținem

copaci ordonată de gradul 2 au un rol deosebit de important. Ele se numesc arbori binari. Definim un arbore binar ordonat ca un set finit de elemente, canete (noduri), fiecare dintre acestea este fie gol sau sostoitiz rădăcină (nod) conectat la două binarnymiderevyami diferite, numit la stânga și la dreapta subramificație rădăcinii. În următoarele paragrafe ale acestei secțiuni, considerăm copaci doar binare și de ce ne consumăm-lyat cuvântul „copac“, însemnând „un arbore binar ordonat.“ Copacii care au un grad mai mare de 2, se numesc ramificare puternic arbori (multiwaytrees). .

Exemple Familiar de arbori binari sunt o familie (familie) copac cu tatăl său și pe mama umană ca și descendenții săi, istoria turneului de tenis, în cazul în care fiecare nod este un joc definit de un câștigător și subarbori - precedentele două jocuri adversari; (!) expresie aritmetică cu operații duble unde kazhdayaoperatsiya este un operanzi de nod ramificare ca subarbori.