aproximare liniară

În prelucrarea datelor experimentale este adesea necesar să se apropie funcția lor liniară.
Apropierea (aproximare) a funcției f (x) este chemat să găsească o astfel de funcție (funcția aproximându) g (x). care ar închide setul. Criteriile pentru funcția de proximitate pot fi diferite.
În cazul în care abordarea se bazează pe un set discret de puncte, apropierea se numește punctul sau discret.
Dacă aproximație se realizează pe un set continuu de puncte (interval), aproximarea se numește continuă sau integrală. Un exemplu de o astfel de aproximare poate servi ca o extindere a seriei Taylor, adică înlocuirea unei funcții a polinomului grade.
Cele mai frecvent întâlnite vedere interpolare punct aproximare este - găsirea valorii intermediare a valorilor care au un set discret de valori cunoscute.
Având în vedere un set discret de puncte, numite noduri de interpolare. și valorile funcției de la aceste puncte. Necesar pentru a construi g funcție (x). care trece cel mai apropiat de toate nodurile specificate. Astfel, criteriul de proximitate este o funcție g (xi) = yi.
Deoarece funcția g (x) este de obicei ales polinomială, cunoscut sub numele de interpolare polinomiale.
Dacă există o interpolare polinomială pentru întreaga regiune, a declarat că interpolarea la nivel mondial.
În cazul în care între diferitele noduri polinoame diferite, indică interpolarea locale sau pe porțiuni.
Găsirea unui polinom de interpolare, putem calcula valoarea funcției între noduri, precum și pentru a determina valoarea funcției, chiar și în afara intervalului specificat (pentru a extrapola).
Apropierea unei funcții liniare
Orice funcție liniară poate fi exprimată prin ecuația
Aproximarea este de a găsi coeficienții a și b din ecuație, astfel încât toate punctele experimentale se află cel mai aproape de apropierea liniei.
În acest scop, cel mai frecvent utilizat metoda celor mai mici pătrate (OLS), dintre care esența constă în următoarele: suma pătratului abaterilor punctului din punctul aproximându ia valoarea minimă:
Soluția problemei se reduce la găsirea extremum a acestei funcții de două variabile. În acest scop, vom găsi derivatele parțiale ale funcției de coeficienții a și b și echivalarea acestora la zero.

Noi rezolva sistemul de ecuații rezultat
Se determină valorile coeficienților

Pentru a calcula coeficienții trebuie să găsiți următoarele componente:
Apoi, valorile coeficienților vor fi definite ca
de exemplu, punerea în aplicare
De exemplu, punerea în aplicare folosim un set de valori obținute în conformitate cu ecuația liniei
Calculăm acești coeficienți prin metoda celor mai mici pătrate.
Rezultatul este stocat sub forma unui tablou bidimensional, format din două coloane.
Data viitoare când porniți programul va adăuga o componentă aleatoare la setul de valori specificat și se calculează din nou coeficienții.
Implementarea în C
_CRT_SECURE_NO_WARNINGS #define
#include
#include
// Setați setul inițial de valori
double ** getData (int n) double ** f;
f = new double * [2];
f [0] = new double [n];
f [1] = new double [n];
pentru (int i = 0; i
// Adăugați componenta aleatoare
f [1] [i] = 8 * (double) i - 3 + ((rand ()% 100) -50) * 0,05;
>
întoarce f;
>
// Se calculează coeficienții liniei aproximându
nule getApprox (x duble **, duble * o, * dublu b, int n) double sumx = 0;
double sumy = 0;
double sumx2 = 0;
double sumxy = 0;
pentru (int i = 0; i
sumx2 + = x [0] [i] * x [0] [i];
sumxy + = x [0] [i] * x [1] [i];
>
* A = (n * sumxy - (sumx * sumy)) / (n * sumx2 - sumx * sumx);
* B = (sumy - * o sumx *) / n;
return;
>
int main () dublu x **, a, b;
int n;
sistem ( "chcp 1251");
sistem ( "cls");
printf ( „Introduceți numărul de puncte“);
scanf ( "". n);
x = getData (n);
pentru (int i = 0; i
getApprox (x, o, b, n);
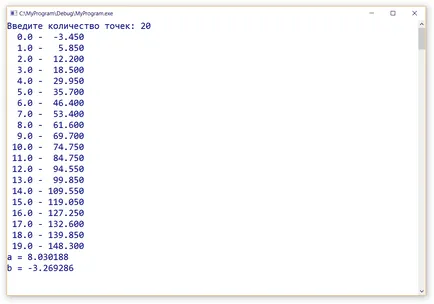
printf ( "a =% lf \ nb =% lf" a, b.);
getchar (); getchar ();
return 0;
>
rezultatul execuției
Rulați nici o componentă aleatoare

Începând cu componenta aleatoare
Trasarea funcții
Implementarea în C
#include
NUM const int = 70; // numărul de puncte
LONG WinAPI WndProc (HWND UINT wParam lParam ...);
x duble **; // array de date
// Determinarea coeficienților aproximarea liniară a OMEN
nule getApprox (double m **, dublu * o, dublu * b, int n) double sumx = 0;
double sumy = 0;
double sumx2 = 0;
double sumxy = 0;
pentru (int i = 0; i
sumx2 + = m [0] [i] * m [0] [i];
sumxy + = m [0] [i] * m [1] [i];
>
* A = (n * sumxy - (sumx * sumy)) / (n * sumx2 - sumx * sumx);
* B = (sumy - * o sumx *) / n;
return;
>
// Setați datele sursă pentru diagramă
// (matrice bidimensională poate cuprinde mai multe rânduri de date)
double ** getData (int n) double ** f;
double a, b;
f = new double * [3];
f [0] = new double [n];
f [1] = new double [n];
f [2] = new double [n];
pentru (int i = 0; i
f [1] [i] = 8 * x - 3 + ((rand ()% 100) - 50) * 0,05;
>
getApprox (f, o, b, n); // aproximare
pentru (int i = 0; i
>
întoarce f;
>
// Desenam grafice de funcții
nule DrawGraph (HDC HDC, RECT rectClient, double x **, int n, int numrow = 1) dublu OffsetY, OffsetX;
double MAX_X = 0;
double MAX_Y = 0;
double ScaleX, ScaleY;
double min, max;
int înălțime, lățime;
int X, Y; // coordonatele ferestrei (în pixeli)
HPEN hpen;
înălțime = rectClient.bottom - rectClient.top;
width = rectClient.right - rectClient.left;
// FIELD valori admisibile X
min = x [0] [0];
max = x [0] [0];
pentru (int i = 0; i
if (x [0] [i]> max)
max = x [0] [i];
>
temp double = max - min;
MAX_X = max - min;
OffsetX = min * latime / MAX_X; // ofset X
ScaleX = (dublu) lățime / MAX_X; // factor scală X
// FIELD valori admisibile Y
min = x [1] [0];
max = x [1] [0];
pentru (int i = 0; i
if (x [j] [i]> max)
max = x [j] [i];
>
>
MAX_Y = max - min;
OffsetY = max * înălțime / (MAX_Y); // ofset Y
ScaleY = (dublu) înălțime / MAX_Y; // factor de scalare Y
// Render axe
hpen = CreatePen (PS_SOLID 0, 0.); // 1px stilou negru
SelectObject (HDC, hpen);
MoveToEx (HDC, 0, OffsetY, 0); // se deplasează punctul (0; OffsetY)
LineTo (HDC, latime, OffsetY); // desen o axă orizontală
MoveToEx (HDC, OffsetX, 0, 0); // trece la punctul (OffsetX; 0)
LineTo (HDC, OffsetX, înălțime); // Desenam o axă verticală
DeleteObject (hpen); // scoate stiloul negru
// Desen graficul funcției
color int = 0xFF; // stilou roșu pentru primul rând de date
pentru (int j = 1; j <= numrow; j++) hpen = CreatePen( PS_SOLID. 2, color); // формирование пера 2px
SelectObject (HDC, hpen);
X = (int) (OffsetX + x [0] [0] * ScaleX); coordonatele // a punctelor de pornire ale graficului
Y = (int) (OffsetY - x [j] [0] * ScaleY);
MoveToEx (HDC, X, Y, 0); // trece la punctul de plecare
pentru (int i = 0; i
LineTo (HDC, X, Y);
>
color = culoare <<8; // изменение цвета пера для следующего ряда
DeleteObject (hpen); // scoate stiloul curent
>
>
// funcție principală
int WinAPI WinMain (HINSTANCE hInstance,
HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow) HWND hwnd;
msg MSG;
WNDCLASS w;
x = getData (NUM); // Setați datele inițiale
memset (w, 0, sizeof (WNDCLASS));
w.style = CS_HREDRAW | CS_VREDRAW;
w.lpfnWndProc = WndProc;
w.hInstance = hInstance;
w.hbrBackground = CreateSolidBrush (0x00FFFFFF);
w.lpszClassName = "clasa mea";
RegisterClass (w);
hwnd = CreateWindow ( "clasa mea", "funcția Graph"
WS_OVERLAPPEDWINDOW. 500, 300, 500, 380, NULL. NULL,
hInstance, NULL);
ShowWindow (hwnd, nCmdShow);
UpdateWindow (hwnd);
în timp ce (getMessage (msg, NULL 0, 0).) TranslateMessage (msg);
DispatchMessage (msg);
>
msg.wParam reveni;
>
// Funcția fereastră
LONG WinAPI WndProc (HWND hwnd, UINT Mesaj,
WParam wParam, lParam lParam) HDC HDC;
ps PAINTSTRUCT;
comutator (Message) caz WM_PAINT:
hdc = BeginPaint (hwnd, ps);
DrawGraph (HDC, ps.rcPaint, x, NUM, 2); // reprezentarea grafică
EndPaint (hwnd, ps);
pauză;
caz WM_DESTROY:
PostQuitMessage (0);
pauză;
default:
întoarce DefWindowProc (hwnd, Mesaj, wParam, lParam);
>
return 0;
>