Apendicele 2 hiperboloid sub formă de foi de rotație - spațiu divin
hiperboloid acoperite cu o prelată
Dacă linia de generare a mișcării este rotit în jurul unei linii drepte fixă (axa) apoi formată în acest caz, suprafața este numita suprafață de revoluție. Linia generatoarea poate fi curbă plană sau spațială și în linie dreaptă.
Fiecare punct al liniei generatoarei în timpul rotației în jurul axei descrie un cerc care se află într-un plan perpendicular pe axa de rotație. Aceste cercuri sunt numite paralele. Prin urmare, un plan perpendicular pe axa de rotație se intersectează la suprafața paralele. Linia de suprafață intersecție de rotație de un plan care trece prin axa este numit un meridian. Toate meridianele sunt congruente cu suprafața de rotație.
O multitudine de paralele sau meridiane este o suprafață continuă a cadrului revoluției. Prin fiecare punct de pe suprafața trece una paralelă și un meridian. Proiecțiile sunt aranjate la punctele respective ale proiecțiilor paralele sau meridiane. Specificați un punct de pe suprafața sau de a construi o a doua proeminență a punctului, în cazul în care unul este setat, puteți utiliza paralel sau meridianul care trece prin acest punct. porțiune determinant geometric al unei suprafețe de rotație a elementului axei de rotație și linia generatoarei.
Suprafețele formate prin rotirea unei linii drepte:
1. - Cilindrul de rotație formată prin rotirea unei linii drepte paralele cu axa;
2. - con de revoluție formate prin rotirea unei linii drepte ce intersectează axa;
3. - hiperboloid de rotație formată sub formă de foi, prin rotirea liniei încrucișate cu axa;
Paralel cu suprafața sunt cercuri.
Meridian a suprafeței este o hiperbolă.
Toate suprafețe cutate este o suprafață de rotație de ordinul al doilea.
Suprafețele formate prin rotirea curbelor de ordinul al doilea în jurul axelor lor
1. Domeniul de rotație este format circumferențial în jurul diametrului său.
2. rotitoare Ellipsoid format prin rotirea unei elipse în jurul axei majore sau minore.
3. paraboloid de rotație generată de rotirea unei parabole în jurul axei sale.
4. hiperboloid de rotație a unei coli este formată prin rotirea în jurul axei sale hiperbola imaginar (această suprafață este, de asemenea, formată prin rotirea unei linii drepte: și n-1.).
Hiperboloid a unei coli este o suprafață, ecuația canonică are forma:
în cazul în care a, b, c - numere pozitive.
El are trei planuri de simetrie, cele trei axe de simetrie și de centrul de simetrie. Ele sunt, respectiv coordonatele plan axa și originea de coordonate. Pentru a construi un hiperboloid găsi secțiunea lui în diferite planuri. Noi găsim linia de intersecție cu xOy avionul. Pe acest plan z = 0, deci
Această ecuație definește un xOy plan pe o elipsă cu semi-axe a și b (fig. 1). Noi găsim linia de intersecție cu planul yOz. Pe acest plan x = 0, deci
Această ecuație pentru o hiperbolă yOz plan, în care axa reală este egal cu b, iar axa imaginară este egal cu c. Construim acest hiperbolă.
Secțiune transversală plană xOz ca hiperbolă cu ecuația
Egal și hiperbola, dar nu supraîncărca liniile suplimentare de desen nu va portretiza asimptota și elimina asimptota planul secțiunii yOz.
Noi găsim linia de intersecție a suprafeței cu planul z = ± h, h> 0.
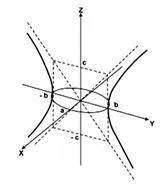
Fig. 1. Secțiune transversală a hiperboloid a unei coli
Ecuațiile acestor linii:
Prima ecuație în forma
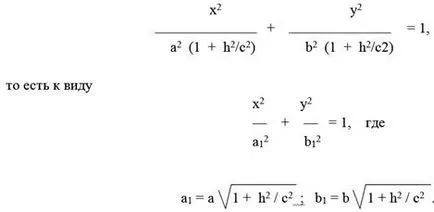
Această ecuație este o elipsă similară cu elipsa în planul xOy, cu un coeficient de similaritate și semiaxes a1 și b1. Desenați o secțiune transversală obținută (Fig. 2).
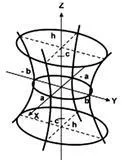
Fig. 2. Imaginea de hiperboloid folosind secțiuni transversale
hiperboloid de rotație sub formă de foaie poate fi obținută prin rotirea liniei drepte a traversat cu axa imaginară în jurul căreia se rotește această linie. În acest caz, o figură spațială (fig. 3), suprafața care constă în pozițiile succesive ale liniei în rotație.
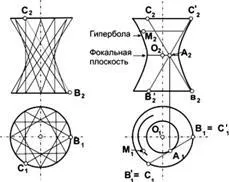
Fig. 3. hiperboloid de revoluție obținută sub formă de foi, prin rotirea unei linii drepte este încrucișat cu axa de rotație
Meridian de o astfel de suprafață este o hiperbolă. Spațiul din interiorul cifra de rotație va fi valabilă, iar la exterior - imaginar. Plan perpendicular pe axa imaginar și taie hiperboloidul de o singură foaie în secțiunea minimă, numit plan focal.
Habitual hiperboloid imagine ochi a unei coli este prezentată în Fig. 6.4.
Dacă în ecuația a = b, atunci avioanele secționate hiperboloid paralele cu planul xOy sunt cercuri. În acest caz, suprafața este numită hiperboloidul rotativ one și sub formă de foaie poate fi obținută prin rotirea hiperbola situată în planul yOz, în jurul axei Oz (Fig. 4).
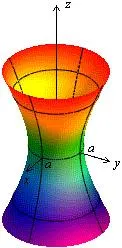
Fig. 4. hyperboloids de rotație, cu prelată