A doua comandă aproximare polinomială, calculul coeficienților de transfer - automată
Modelul este descris de o ecuație ordinea de forma:
Pentru a găsi coeficienții a, b, c, care îndeplinește toate condițiile obiectului formează sistemul de reglare al doilea ecuatiei, numărul de ecuații în sistem este numărul de stări ale obiectului în experiment:
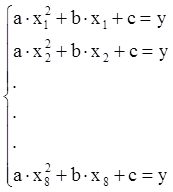
Pentru a rezolva sistemul de ecuații algebrice folosim metoda celor mai mici pătrate cu matrice. Forma matricea semnalelor de intrare și de ieșire:
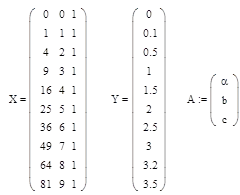
Obținem un sistem cu trei necunoscute: X. A = Y
Noi rezolva ecuația matrice:
unde A - matricea de ordinul doi coeficienți polinomiali.
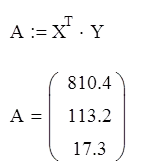
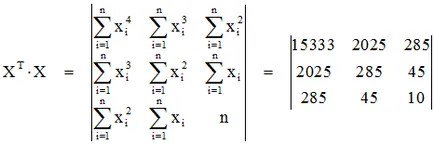
Obținem un sistem de trei ecuații algebrice
Decizia de aceasta, vom determina coeficienții a, b, c.
Am găsit principalul factor determinant al sistemului:
Noi găsim factorii determinanți ai sistemelor auxiliare:
Să ne găsim coeficienții a, b, c:
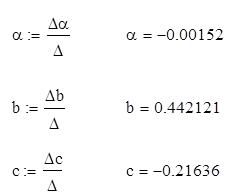
Astfel, avem de ordinul al doilea polinom:
y = -0.00152. xi 2 + 0.442121. xi -0.21636
Pentru a calcula valoarea de evaluare obținută prin funcții polinomiale și le compară cu datele experimentale:
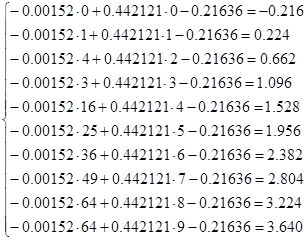
Rezultatele sunt rezumate în Tabelul 3
Suma pătratelor abaterilor este egală cu: yi 2 = 0.173
Ceea ce urmează este un calcul al modelului de verificare a obiectului de ordinul întâi pe un sistem informatic în MathCad.

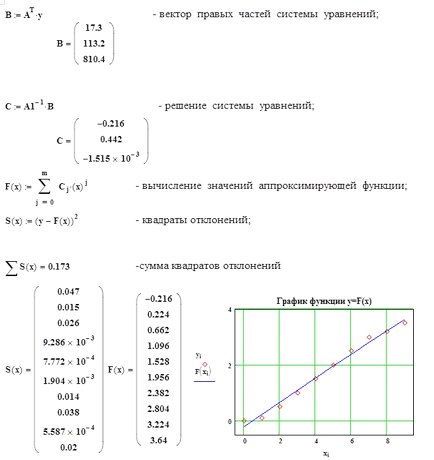
Comparând suma pătratului abaterilor arată că polinomul de ordinul doi este doar ușor descrie mai fidel comportamentul obiectului decât polinomul de prim ordin. Din care rezultă că comportamentul unui obiect se supune ecuația foarte aproape de linia ecuație. Pentru calcule folosind ecuația găsită de polinomul de ordinul doi.
Calculul coeficienților de transmisie
Pentru un model static al primului factor de transmisie comandă este definit ca derivat al variabilei de ieșire:
Coeficientul de transfer obiect indică în ce direcție și în ce măsură există o schimbare de semnal atunci când trece printr-un obiect, adică proprietățile de armare ale unui obiect.
Pentru un model static al primului factor de transmisie comandă este definit ca derivat al variabilei de ieșire:
Pentru modelul static al doilea coeficient de transfer de comandă este definit ca derivata variabilei de ieșire:
Calcularea coeficienților efectuate la transmiterea de 10, 50 și 90%
Se calculează valoarea coeficientului de transmisie de 10%, conform formulei:
în cazul în care - valoarea maximă a semnalului de echilibru.
- semnalul minim de valoare.
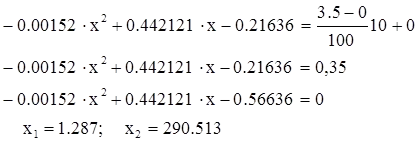
Substituind aceste date, obținem:
Alege x1, pentru că odată ce intră în intervalul valorilor experimentale. Valoarea suplean x1 (1.2) și se obține valoarea câștigului la 10% din funcționare nominală:
Se calculează valoarea câștigului la 50%, prin formula:
Substituind aceste date, obținem:
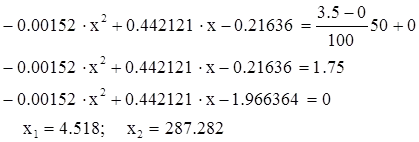
Alegeți x1. adică. în momentul în care intră în intervalul valorilor experimentale. Substituind valoarea x1 în (1.2) și se obține valoarea câștigului la 50% din modul nominal:
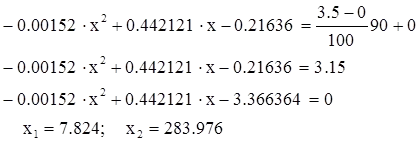
Se calculează valoarea coeficientului de transmisie de 90%, conform formulei:
Alegeți x1. adică. în momentul în care intră în intervalul valorilor experimentale. Valoarea suplean x1 (1.2) și se obține valoarea câștigului la 90% din modul nominal:
Rezultatele calculului în tabel.