20A viteza de zbor
DETERMINAREA VITEZEI corpul ZBOR folosind pendulului de torsiune balistică
Tselraboty. Învățarea pentru a determina experimental viteza de mișcare a corpurilor.
Baza determinării experimentale a vitezei de zbor a corpului cu un pendul balistic este legea conservării momentului cinetic.
E
în care r - cea mai mică distanță de axa pendulare la traiectoria de mișcare a corpului. In timpul fotografierii pendulul este în repaus, și anume, impulsul său unghiular este zero. După atașarea la corpul vasului de pendul, împreună cu corpul capătă o viteză unghiulară inițială 0.
Din legea conservării momentului cinetic pentru un sistem al organismului - pendulul rezultă că
I1- unde momentul total de inerție al pendulului și axa de rotație a corpului. Pendulul 0 cu viteza unghiulară și, respectiv, energia cinetică
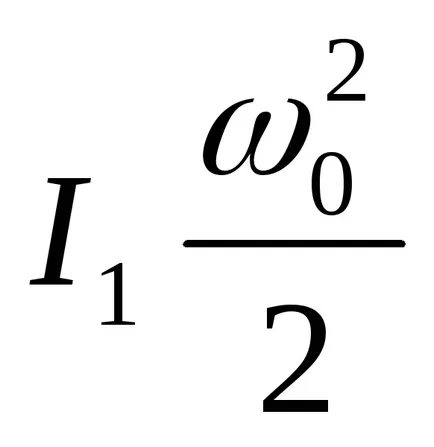
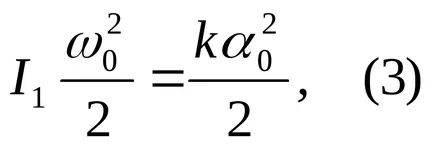
în care k- coeficientul de elasticitate filament; Unghiul α0 pendulului maxim de torsiune.
Rezolvarea ecuației (2) și (3) găsim
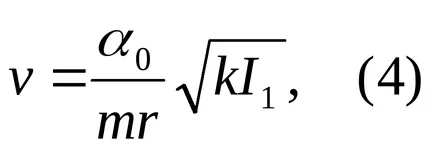
Pentru a determina viteza V (4), este necesar să se cunoască valorile k și I1. Pentru a face acest lucru, efectuați două măsurare suplimentară în baza legilor oscilațiilor torsionale ale pendulului.
Din a doua lege a dinamicii pentru mișcarea de rotație ar trebui să fie
unde - accelerația unghiulară a unui pendul;
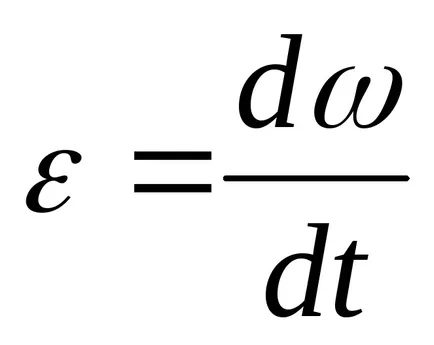
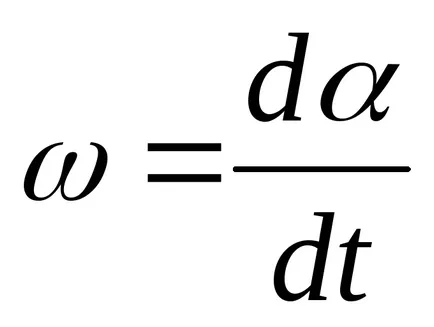
Astfel, ecuația oscilațiilor de torsiune ale pendulului (5) este convertit în forma;
unde
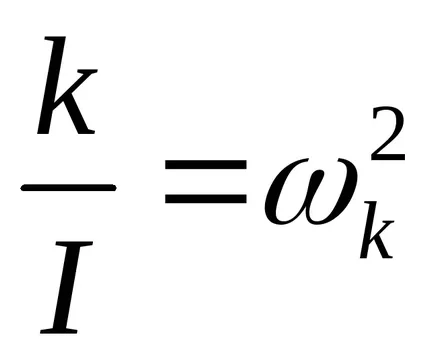
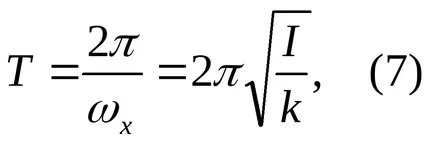
Perioada de oscilație a pendulului poate fi găsit experimental, perioada va depinde de momentul de inerție al pendulului și coeficientului k elastic al suspensiei.
Schimbarea momentul de inerție al încărcăturii M masa pendulului se deplasează din poziția R1, pentru care momentul I1 inerție. în poziția R2. pentru care momentul I2 inerție și definind aceste perioade puncte T1 și T2. Noi alcătuiesc sistemul (Figura 1)
în cazul în care I0 - momentul de inerție al sistemului fără bunuri în mișcare;
Rezolvarea sistemului de ecuații, constatăm că coeficientul de elasticitate fire
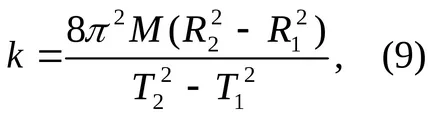
și momentul de inerție
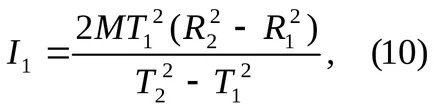
Substituind valorile k și I1 în expresia (4), determină viteza aerului corp
Așa cum este utilizat în instalația prezentată în figurile 1, 2, 3 și include în componența sa: baza 1, montantul 2, superioară W și inferioare 4 paranteze, suportul de mijloc 5, un set de „proiectile“ diferite mase, arc set set dispozitiv de declanșare probe de testare. Baza 1 este prevăzută cu trei suporturi reglabile b și clemă 7 pentru fixarea rack. Un raft vertical 2 este realizat dintr-o țeavă de metal. Upper W și inferioare patru paranteze sunt folosite pentru montarea ansamblurilor de suspensie și tensionarea torsiune 8 (sârmă de oțel), care este conectat cu cadrul metalic 9 cu sarcini 10 (vezi. Fig. 2) destinate pentru montarea unui obiectiv detașabil 11 cu contragreutatea 12 (a se vedea. Figura . 2) și probele de testare 13 (vezi. fig. 3). În medie, consola 5, pe care este aplicat un unghi de răsucire gama de referință al torsiunii aranjate: coborator 14, destinat producției de „shot“, un electromagnet 15 pentru susținerea cadrului în poziția sa de repaus și eliberarea (în timp ce există vibrații torsionale cadrul din jurul ver- axa tikalnoy), un fotosenzor 16 pentru detectarea perioada de oscilație a specimenelor cadru metalic fără ele. Obiectivul detașabil 11 este destinat pentru contactul cu „cochilii“, după împușcat.
Determinarea vitezei de zbor, „coajă“, printr-un pendul balistic de torsiune.
1) Efectuați reglarea poziției de bază de instalare cu suporturile de reglare. Setare țintă în cadrul 9. Asigurați-vă că obiectivul este pe „împușcat“ a liniei, și verificarea cadrului intersectează axa optică a fotosenzorul (frame stocat în poziția inițială). Conectați setările fotoelectrică și o consola centrală electromagnet pentru a bloca e-mail utilizând un cablu. Plug marcat „F“ pentru a insera în soclu fotosenzorul, iar mufa marcată „E“ în priza unui electromagnet. Stabilirea unui „shell“ pe tija de ghidare a trăgaciului 14 cocoș primăvară. Efectuați o „lovitură“. determină vizual unghiul maxim de deviere a deplasării unghiulare cadru scală folosind un steag montat pe cadru.
2) Respinge cadru la un unghi de 30 de grade și sigure prin electromagnetul 15 prin apăsarea REȚEAUA „bloc. Apăsați pe butonul „Start“ bloc. Conform timer-ul blocului mărturie pentru a determina valoarea interval de timp de zece oscilație prin apăsarea butonului „STOP“. Se determină valoarea medie a perioadei de cadre oscilații prin formula:
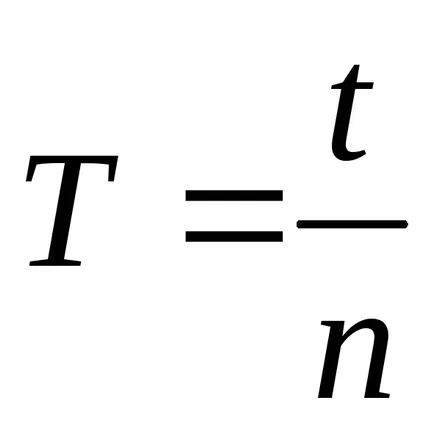
unde t - oscilații în timp, s; n - numărul de vibrații.
3) Apasati "RESET" bloc. Pentru a elimina sarcini din cadrul, repetați operațiile de mai sus și se calculează perioada de oscilație T zece cadre fără încărcătură formula n 2. Se calculează viteza de zbor „proiectil“ formulă .:
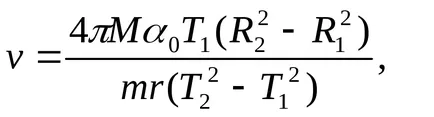
în care (0 - deformarea maximă a cadrului unghi rad R1 = 0,0525 m - distanța de la axa de rotație a cadrului către centrele de masă ale mărfurilor, m M - masa sarcinii, kg (cântărește solzi). m - masa „proiectil“ kg (cântărite pe cântare), T2 și T1 - perioadele de oscilație a unui cadru cu bunuri și fără ele, cu R2 - distanța de la axa de rotație a cadrului de „coajă“ centru de amprente, o blocat în ținta (măsurată cu o riglă) și de a efectua cel puțin trei. „fotografii“ și se calculează rata medie de „proiectil“.
4) Eroare Rate de măsurare indirectă „proiectil“ de viteză cu ajutorul formulei:
întrebări de control și sarcini
1. Statul legea conservării impulsului.
2. Care este cuplul?
3. Definiți momentul de inerție în raport cu o axă fixă de rotație.
4. Definiți momentul impulsului unui organism, și să specifice legea conservării momentului cinetic pentru un sistem închis.
5. Notați ecuația fundamentală a dinamicii mișcării de rotație.
6. Înregistrarea formulei energiei cinetice a unui corp de rotație în jurul unei axe fixe.
7. Se înregistrează formula operație cu mișcarea de rotație a corpului.