11 seminar
Curbele de a doua comandă în avion.
fundal
I. Ecuația unei linii în avion.
linia Opredelenie.Uravneniem (curba) în planul
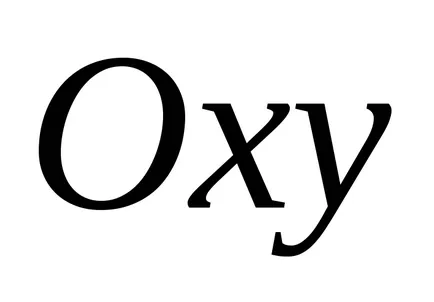

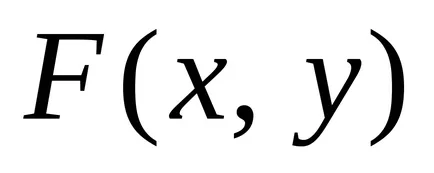


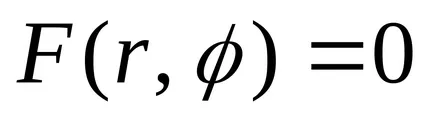
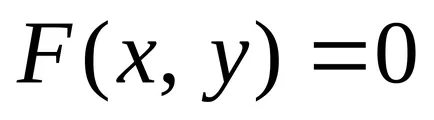

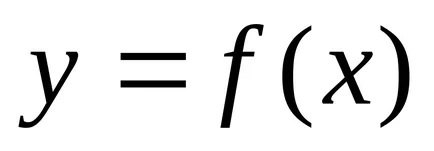
Deoarece coordonatele unui punct de pe linia conectată prin ecuația, linia este unidimensională obiect geometric. Problema găsirii punctelor de intersecție a celor două linii de date de ecuațiile

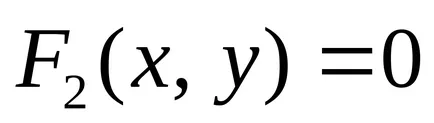
se reduce la rezolvarea unui sistem de două ecuații cu două necunoscute:
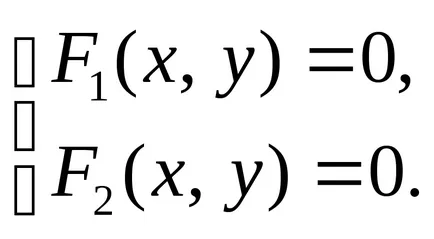
Linia pe planul poate fi, de asemenea, specificate parametric folosind două ecuații
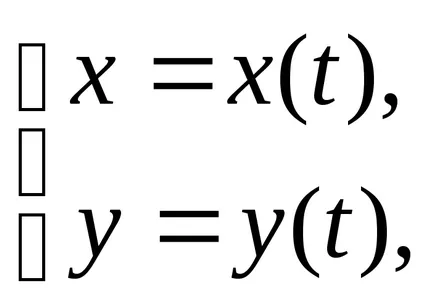
unde
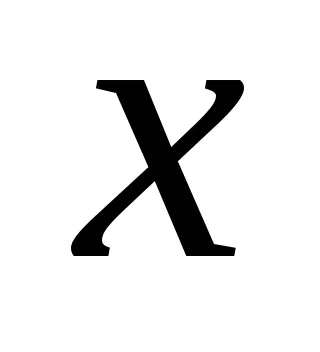

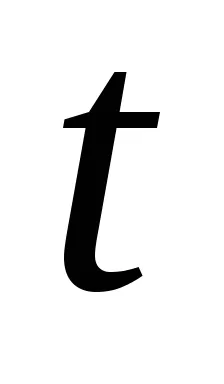
Acestea sunt câteva exemple de linii.
raza cercului
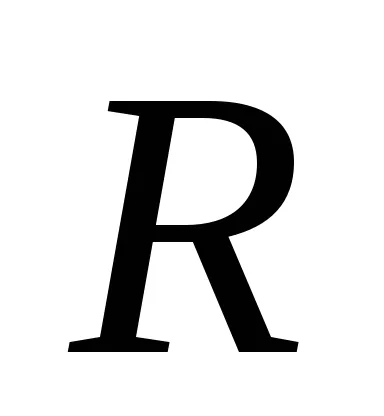
Ecuațiile astfel un cerc au forma:
a)
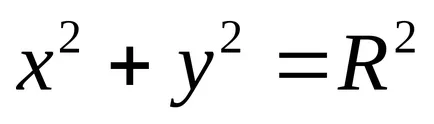
b)
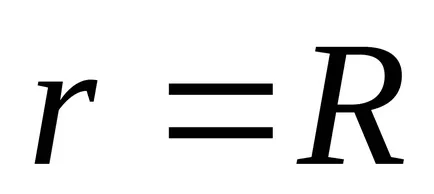
c)

Forma parametrică a ecuației cicloida are forma
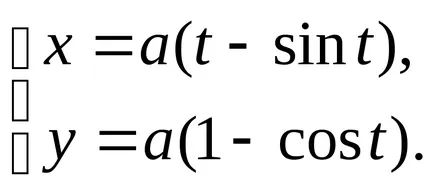
Acesta descrie un punct de curbă pe un cerc de rază

Astroidă dată de ecuațiile:
a)
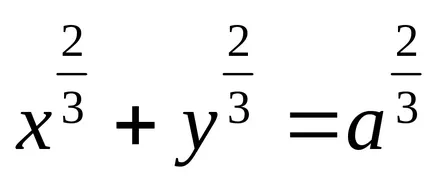
b)
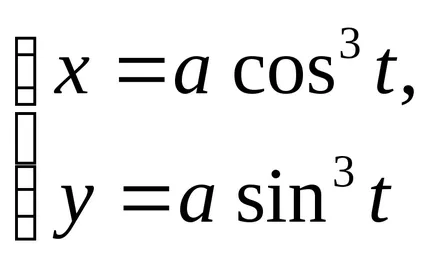
Acesta descrie un punct de curbă pe un cerc de rază
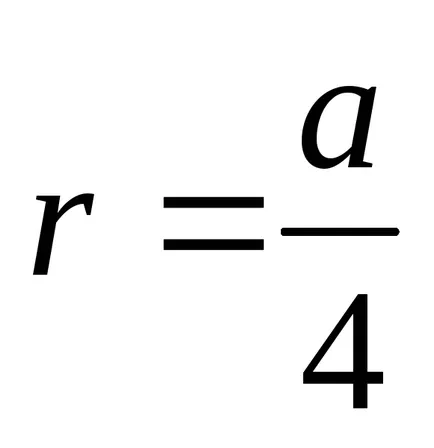
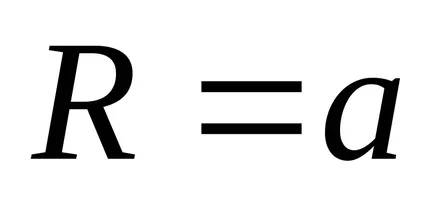
Ecuația coordonate polare cardioidă este dată de
.
Această curbă descrie un cerc de rază punctului
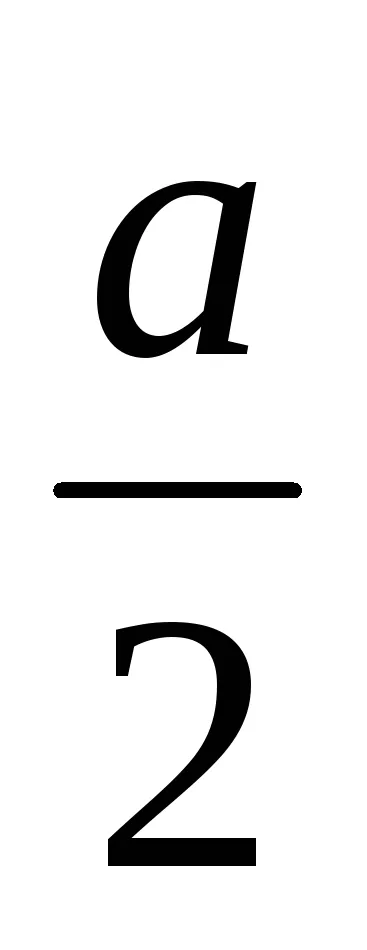
Ecuația cardioid este un caz special (
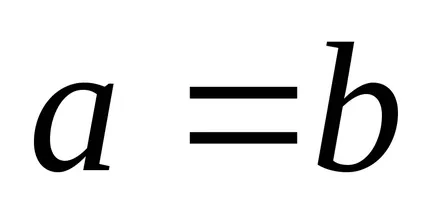
.
lemniscate Bernoulli dată de ecuațiile:
a) - într-un sistem de coordonate carteziene;
b)
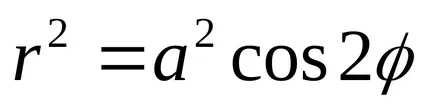
Produsul a distanțelor de la fiecare punct de lemniscate Bernoulli la două puncte de date
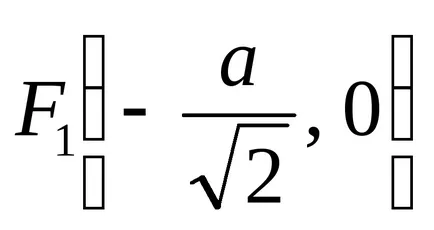
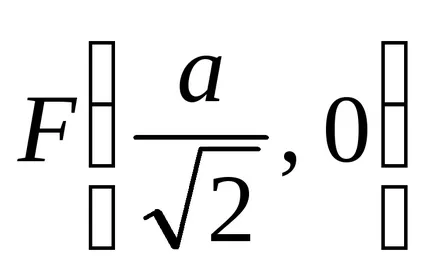


foaie cartezian dată de ecuațiile:
a) - într-un sistem de coordonate carteziene;
b)
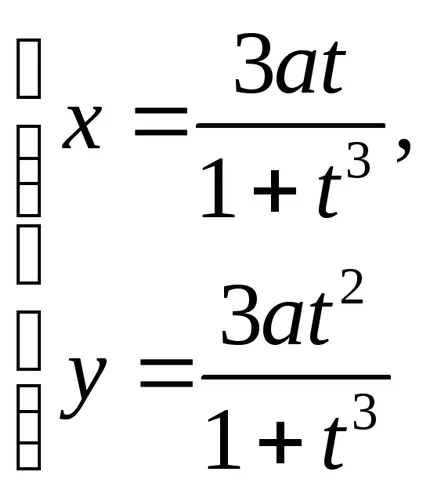
Forma parametrică a curbei este dată de ecuațiile
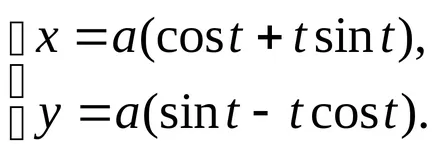
9) a crescut de trei ori.
această curbă în sistemul de coordonate polare definită de ecuația
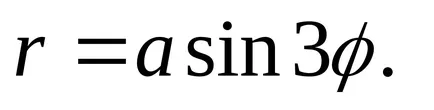
10) chetyrehlepestkovaya a crescut.
Ecuația ei are forma
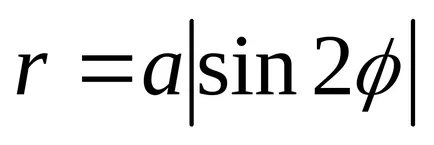
11) o spirală de Arhimede.
Această curbă în sistemul de coordonate polare este descris de ecuația
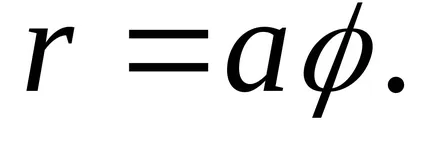
12) o spirală logaritmică.
Ecuația ei are forma
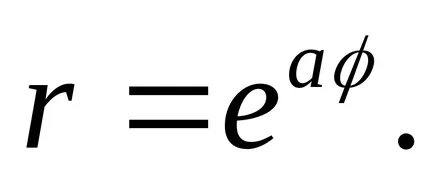
13) spiral hiperbolice.
Această curbă este dată de ecuațiile
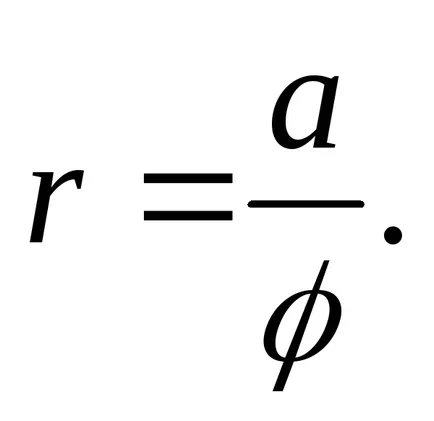
II. Ecuația generală a doua comandă și aducerea la forma canonică.
Ecuația generală de ordinul doi al liniei are forma
Se presupune că
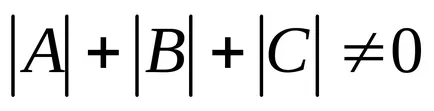
Traducere paralel cu originea.
Nou (amorsate) a introdus un sistem de coordonate cu ajutorul relațiilor

În noul sistem de coordonate, ecuația (1) devine
Luând ca constante
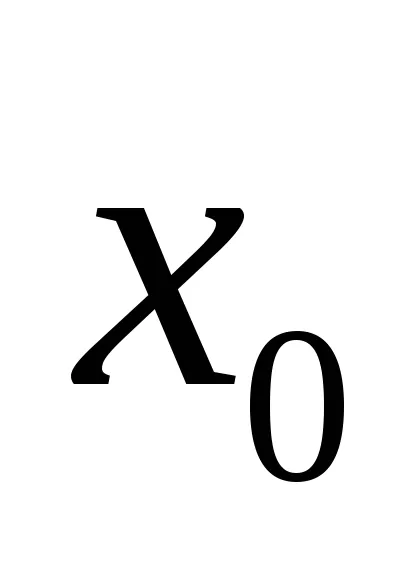
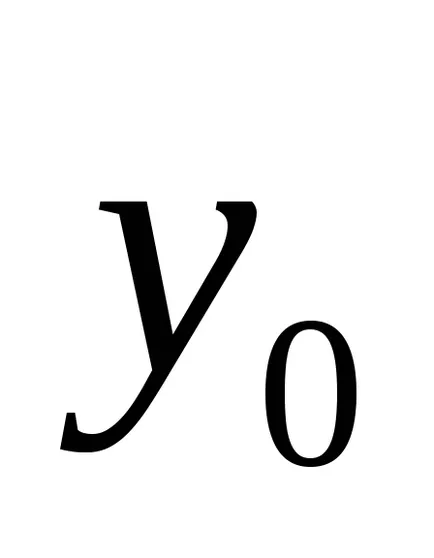
putem elimina din ecuația curbei cu termenii primelor variabile de gradul
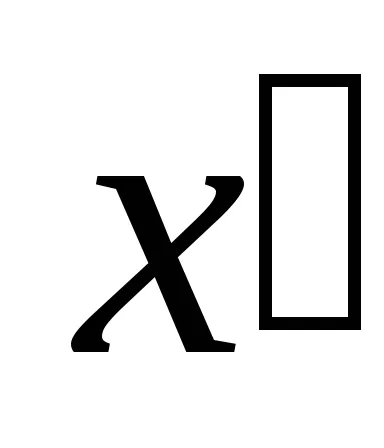


La rezolvarea sistemului de ecuații (2) cazuri posibile:
1)
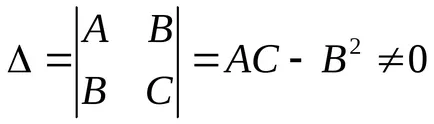
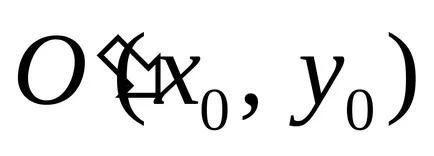
2). Pot exista cazuri:
a) sistemul de ecuații nu are nici o soluție, curbele nu au centrul și numit parabole;
b) sistemul de ecuații are un număr infinit de soluții, curba este numită parabole degenerate (sau o pereche de linii paralele imaginare ale unui punct).
În continuare, ia în considerare cazul detaliilor curbe centrale. Facem rotirea axelor de coordonate de unghiul

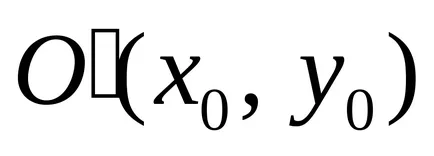
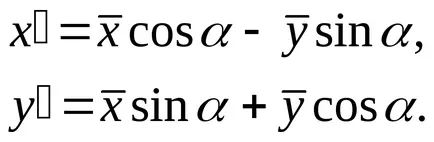
Curba de ecuația (3) devine
,
Am ales unghiul de rotație a axelor de coordonate

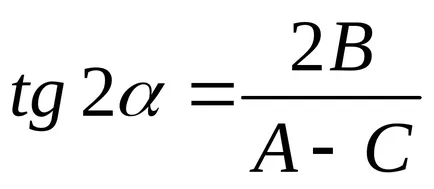
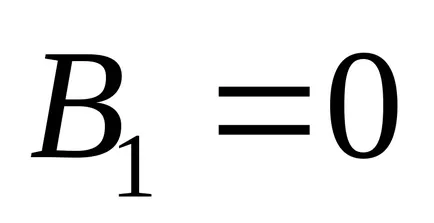
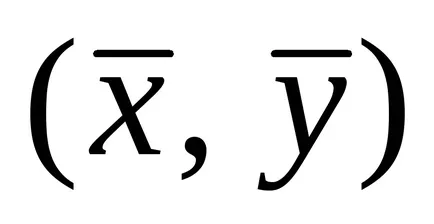
.
Exemplu. Să ecuația forma canonică a doua curbă comandă, pentru care. Găsim coordonatele centrului curbei sistemului de ecuații


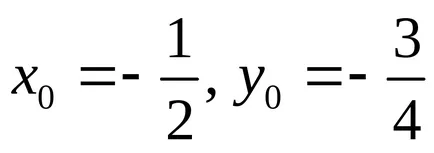
.
Rețineți că pentru dată, adică curba curba este o elipsă. Rotiti axele de coordonate printr-un unghi

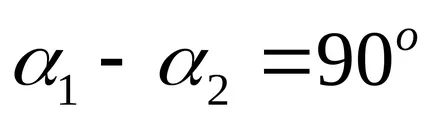
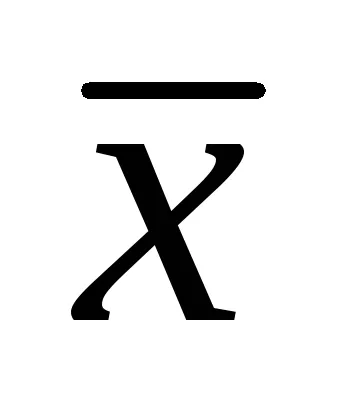




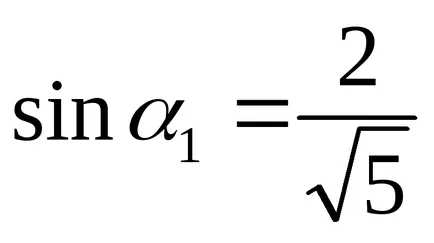

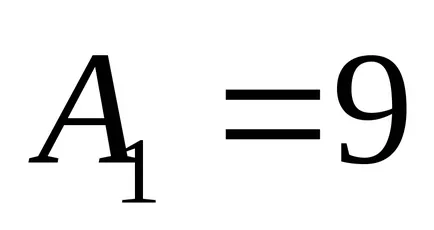
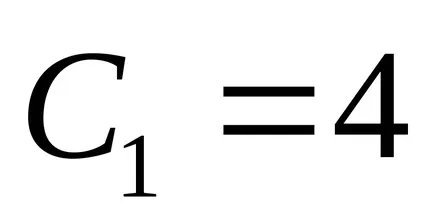
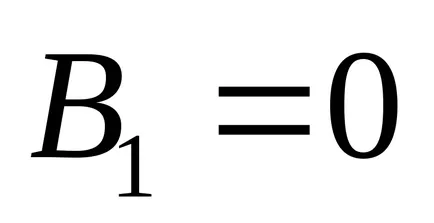
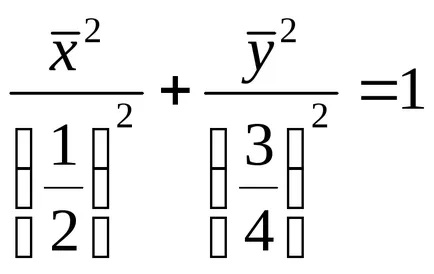
Avem ecuația canonică a unei elipse cu semi-axe