1-0, 378 * (E
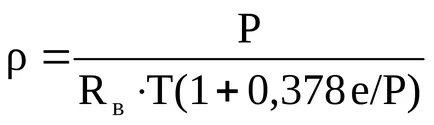
Temperatura Cantitatea nazyvaetsyavirtualnoy (Tv).
.
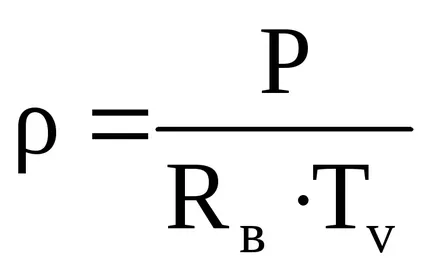
adică densitatea aerului umed este descrisă de ecuația de stare a aerului uscat, dar cu înlocuirea temperaturii T la un televizor temperatură virtuală.
Virtual Tv Temperatura aerului umed - este acea temperatură care ar trebui să fie aer uscat la o densitate egală cu densitatea aerului umed cu temperatură T. presiune P și presiunea vaporilor de apă e.
Temperatura virtuală este întotdeauna ușor mai mare decât temperatura reală a aerului umed.
densitatea aerului la fiecare locație se schimbă continuu în timp. În plus, aceasta variază în înălțime, deoarece înălțimea variază ca presiunea atmosferică și temperatura aerului. Presiunea cu înălțimea scade mereu, și scade densitatea și împreună cu ea. Temperatura cu altitudinea, miezul este redus cu cel puțin în straturile inferioare (10-15 km) atmosfera. Dar scăderea temperaturii determină o creștere a densității. Ca urmare, impactul general al modificărilor presiunii și temperaturii, cu o densitate de altitudine este în general redus, dar nu atât de mult ca și presiunea. În medie, pentru Europa este egal la suprafața de 1,25 kg / m 3; la o înălțime de 5 km - 0.74 kg / m 3; 10 km - 0.41 kg / m 3; 20 km - 0.09 kg / m3.
schimbare a presiunii aerului cu înălțimea. formula barometric
Legea conform căreia schimbările de presiune atmosferică cu altitudinea?
Să presupunem că știm presiunea la același nivel. Ce este, în același timp, la un nivel diferit? Să considerăm o coloană verticală a aerului, cu o secțiune transversală egală cu una, și selectați coloana dintr-un strat subțire, delimitat de suprafața inferioară la Z. înălțime și deasupra - în înălțimea suprafeței (Z + dZ). Grosimea stratului dZ.
Figura 3.1 - forțe care acționează asupra unui volum elementar de aer
Pe suprafața inferioară a elementului de volum selectat actele de aer adiacente cu forță de presiune care îndreptate în sus. Modulul acestei forțe pe suprafața considerată egală cu unul, și va fi presiunea aerului P pe suprafață. Pe suprafața superioară a volumului elementar actelor aeriene adiacente cu o forță de presiune care este îndreptată în jos. Modulul acestei puteri P + dP este presiunea la limita superioară. Această presiune diferă de presiunea la limita inferioară de pe DP-dimensiuni mici, în cazul în care nu este cunoscută în avans, DP este pozitiv sau negativ, atunci va exista o presiune asupra limita superioară este mai mare sau mai mică decât limita inferioară.
În ceea ce privește forțele de presiune care acționează asupra peretelui lateral al volumului, apoi presupune că presiunea atmosferică nu se schimbă în direcția orizontală. Acest lucru înseamnă că forțele de presiune care acționează asupra ambelor părți în pereții laterali, sunt echilibrate: rezultanta lor este zero. Acest lucru implică faptul că aerul nu are nici o accelerație și nu este deplasat în direcția orizontală.
De asemenea, este considerat un element de volum forța de gravitație, și care este egală cu accelerația descendentă datorită gravitației g, ori masa aerului luată în cantitate. Prin urmare, atunci când secțiunea verticală este egal cu unitatea, volumul este egal cu dz, masa aerului în ea este egal cu ρdz, unde ρ - densitatea aerului, și gravitatea gρdz egal.
gravitație Gρdz și forța presiunii P + dp orientată în jos; ia-le cu un semn negativ. Îndreptat în sus forță de presiune P, va lua un semn „+“.
Într-o stare de echilibru:
- (P + dp) + P - gρdz = 0
sau dp = - gρdz (3.4)
Acest lucru implică faptul că, atunci când se deplasează în sus, presiunea atmosferică scade.
Ecuația (3.4) este ecuația fundamentală a atmosferei statice.
-
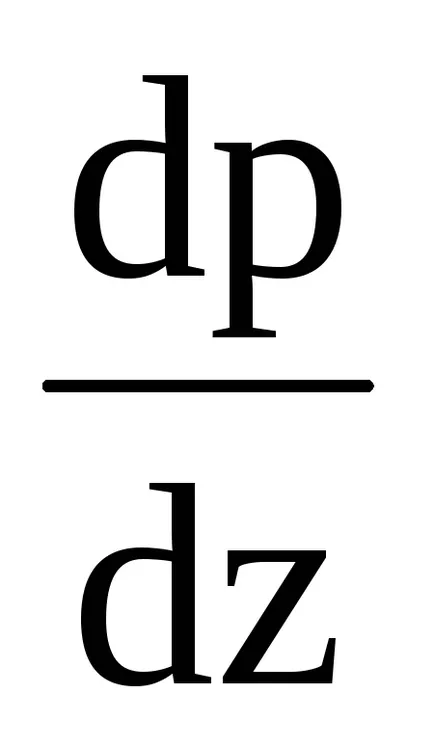
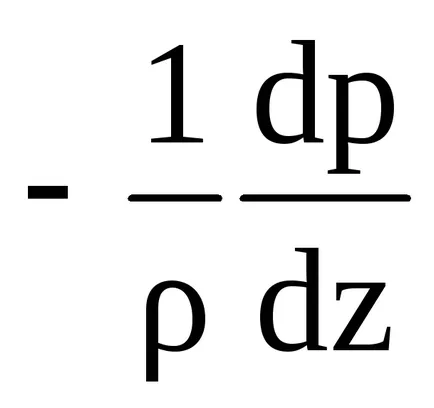
Ecuația de bază exprimă starea de echilibru static între cele două forțe, care acționează asupra unității masa de aer vertical - gradient de presiune verticală și gravitate.
Pentru a obține o ecuație de schimbare a presiunii la incrementul finală a înălțimii este necesară integrarea ecuației (3.4), în intervalul de la z1 nivel la z2 cu presiunea de la P1 la P2. În acest caz, are densitatea aerului care p o variabilă, în funcție de înălțime.
Integrați ecuația (3.5)
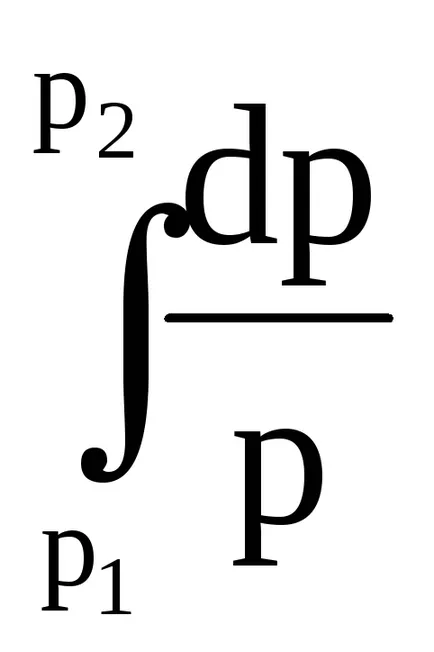
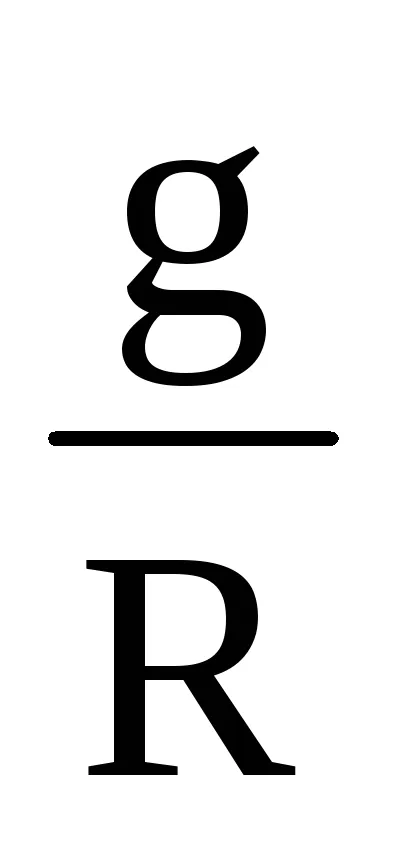
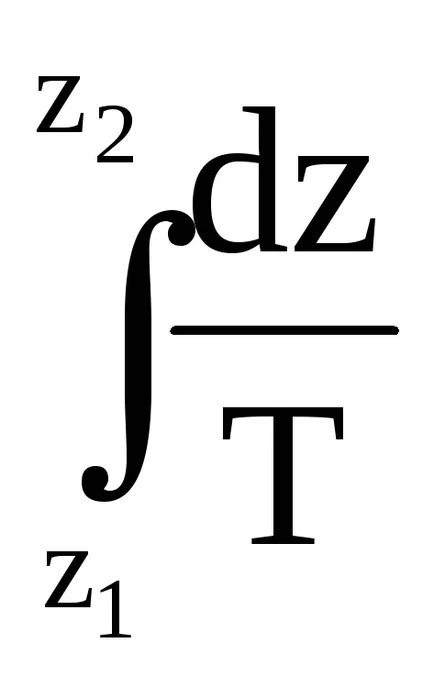
Temperatura - cantitatea de schimbare depinde de altitudine. Dar această relație nu poate fi descris cu exactitate printr-o funcție matematică. Prin urmare, luând valoarea medie a Tm între nivelurile de temperatură ale z1 și z2. Apoi, temperatura medie poate fi luată în afara semnului integrală.
ln
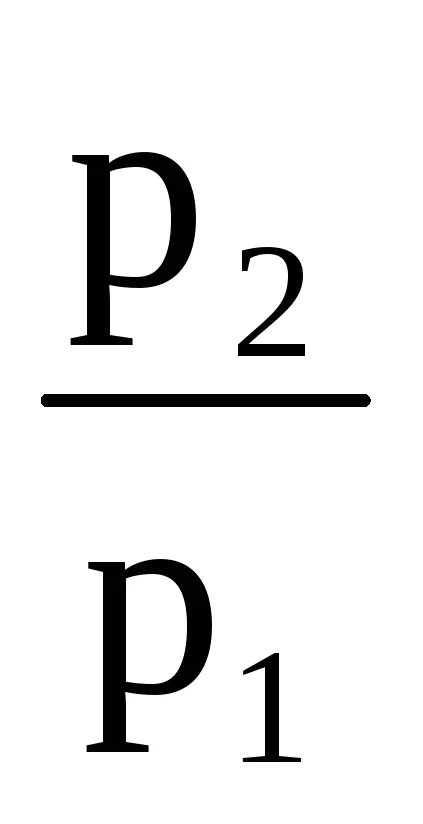
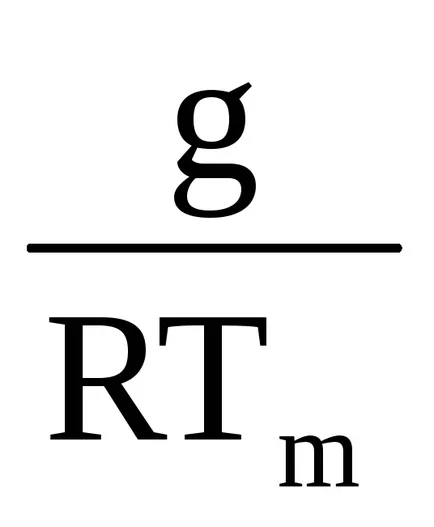
Potențând ecuația 3.6, și obținem:
Ecuația (3.7) se numește formula barometric.
Această formulă arată modul în care presiunea aerului variaza cu altitudinea, în funcție de temperatura exterioară.
Cu ajutorul formulei barometrice poate rezolva trei probleme:
cunoscând presiunea la un nivel și temperatura medie a stratului de aer, găsiți presiunea la celălalt nivel;
cunoscând presiunea pe ambele nivele și temperatura medie a stratului de aer, găsi o diferență de nivel (nivelare barometrică);
știind diferența de nivel și valorile de presiune asupra acestora pentru a găsi temperatura medie a stratului de aer.
În cazul calculelor pentru aerul umed este luat valoarea R pentru aer uscat, înmulțit cu (1 + 0,378)
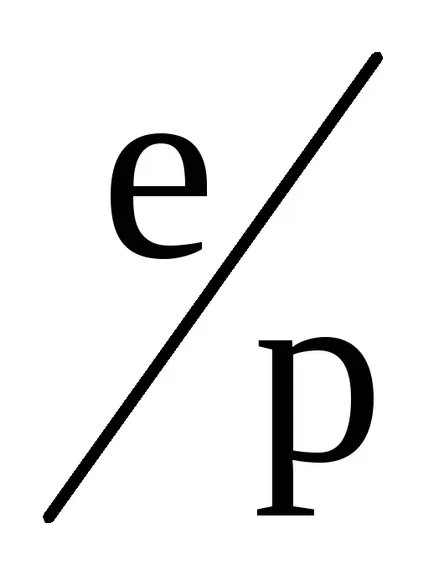
Ea trebuie să aducă o presiune la nivelul mării importantă realizare a primei probleme. Cunoașterea presiunii într-o stație situată la o înălțime Z deasupra nivelului mării, iar temperatura t la această stație, calcularea primei temperaturi medii pe stație și examinată la nivelul mării. Pentru stația de niveluri luate temperatura efectivă și pentru nivelul mării - aceeași temperatură, dar a crescut în măsura în care temperatura medie a aerului variaza cu altitudinea. gradient de temperatură medie pe verticală în troposferă este luată egală cu 0,6 ° C / 100 g
Astfel, în cazul în care o stație are o înălțime de 200 m și temperatura în ea de 16 ° C, apoi la mare temperatură nivel se presupune egală cu 17,2 ° C iar temperatura medie va fi ° C 16,6 După aceea, presiunea la gară și la temperatura medie a presiunii determinată rezultată la nivelul mării. Aducerea presiunii la nivelul mării este necesară, deoarece pe graficul de suprafață meteo se aplică întotdeauna presiune redusă la nivelul mării. Aceasta elimină influența variațiilor în înălțimi ale stațiilor asupra valorii presiunii și devine posibilă pentru a determina distribuția presiunii pe orizontală.