03 Curs
Scopul conversiei circuitelor electrice.
În mod clar distincția porțiuni cu conexiuni seriale și paralele, atunci când se analizează circuitul mixt.
Pentru a putea transforma compusul într-un triunghi stea echivalent și înapoi.
Pentru a fi capabil de a converti sursa de tensiune în sursa de curent și vice-versa.
schemele de conversie a circuitelor.
Pentru conversia circuitelor electrice este simplificarea lor, este necesar din motive de simplitate și comoditate de calcul.
Unul dintre tipurile de bază de conversie a circuitelor electrice este elemente compuse circuite de conversie mixte. Elemente de conexiune mixte - o combinație de conexiuni seriale și paralele, și care vor fi luate în considerare la începutul acestui curs.
Fig. 3-1 arată circuitul ramură în care rezistența R1 sunt conectate în serie. R2, ..., Rn. Prin toate aceste rezistențe trece același curent I. Tensiunile la părțile individuale ale lanțului este notat cu U1. U2, ..., Un.
Fig. 3-1 O conexiune serie.
Deoarece tensiunea la ŽNK ramură
Rezistența tuturor părților din această ramură

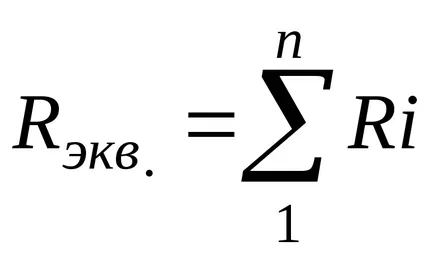
Se numește rezistența echivalentă serie.
Deoarece tensiunea care cade pe rezistențele individuale, aceste rezistențe sunt proporționale, se poate spune că o conexiune serie de rezistență a forma un „divizor de tensiune“. Conceptul de divizorului de tensiune este utilizat pe scară largă în domeniu.
Fig. 3-2 prezintă o diagramă de circuit a două noduri, între care este inclus n paralel cu ramurile admittances G1. G2, ..., Gn. Tensiunea între nodurile U, este aceeași pentru toate ramurile.
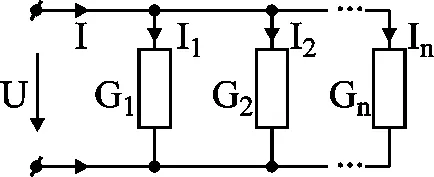
Figura 3-2 conexiune paralelă (reprezentat transformată).
Potrivit totalul NTA este suma curenților de ramuri individuale:
Suma Conductivitatile tuturor ramurilor conectate în paralel
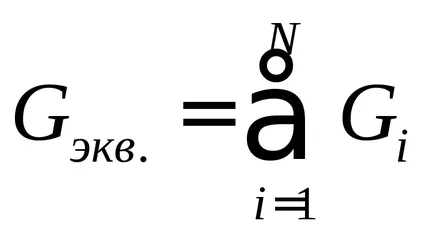
Se numește conductivitate echivalentă.
În cazul rezistenței în paralel a două ramuri (n = 2) expresiile utilizate de obicei, care includ rezistența
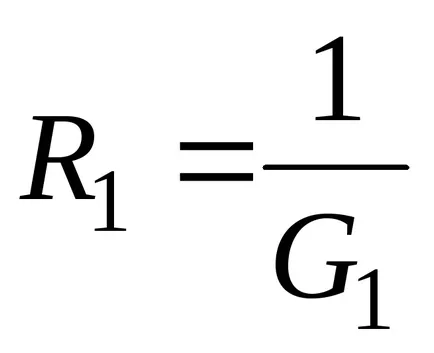
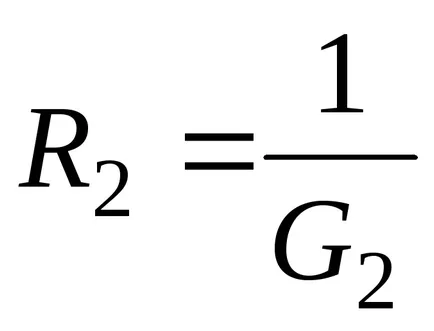
Rezistența echivalentă a celor două ramuri conectate în paralel este:
Deoarece curentul totală este împărțit în ramuri separate curenților proporțional cu conductivitatea acestor ramuri (sau, echivalent, este invers proporțională cu rezistențele acestor ramuri), se poate spune că rezistența formei conectat în paralel un „curentii divizor“. Conceptul de divizor curent utilizat în domeniu.
De multe ori, atunci când se utilizează „manual“ circuitele de calcul trebuie să determine modul în care curentul este împărțită pe ramuri separate ale ramurilor paralele conectate.
Din formula (2), că ramurile curente conectate în paralel este proporțională cu conductivitatea acestor ramuri, adică Curenții sunt împărțite peste ramurile proporționale cu rezistența acestor ramuri, sau, echivalent, este invers proporțională cu rezistența acestor ramuri.
În cazul a două rezistență paralele conectate din rezistența totală (2) este:
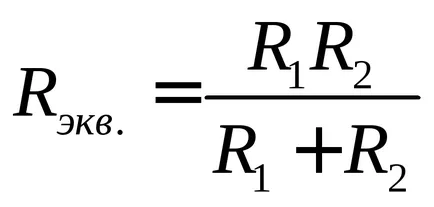
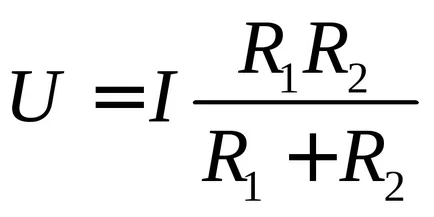
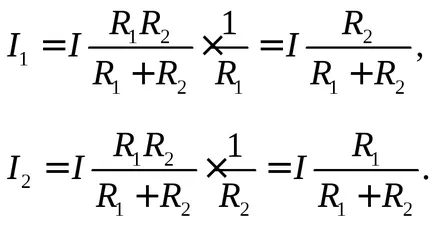
Expresiile obținute pentru curenții numite uneori „regula umăr“, care prevede curent este împărțit între rezistențe legate în paralel (un separator de curent) este invers proporțională cu aceste rezistențe.
În Figura 3-3 prezintă un circuit electric compus mixt:
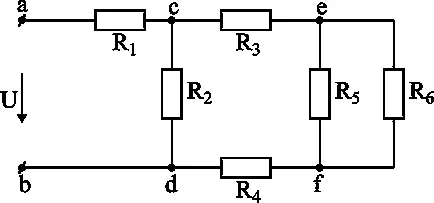
Figura 3-3 Compus mixt.
Acest circuit este ușor de redus la un singur circuit. Rezistența la R5 și R6 sunt conectate în paralel, astfel încât este necesar să se calculeze rezistența echivalentă a porțiunii cu formula

poate fi reprezentat de un cadru provizoriu pentru înțelegerea rezultatelor obținute (Fig. 3-4).
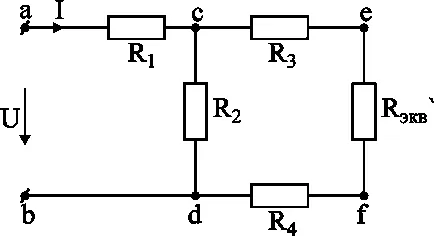
Rezistență R3. R4 și R / echiv. conectate în serie, porțiunea de rezistență echivalentă și c-e-f-d este egal cu:
După această transformare de fază ia forma unei diagrame în Fig. 3-5.
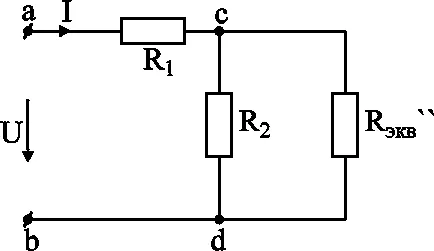
Apoi vom găsi rezistența echivalentă a porțiunii c-d și suma cu rezistența R1. Rezistența totală echivalentă este egală cu:
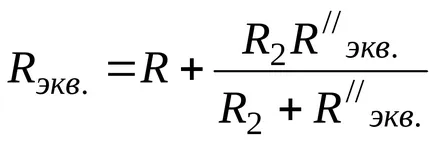
rezistență la primit rezistență echivalentă (fig. 3-6) compus mixt de circuit original. Termenul „echivalent“ înseamnă că tensiunea la bornele de intrare U și curent de ramură de intrare rămân neschimbate pentru toate transformările.
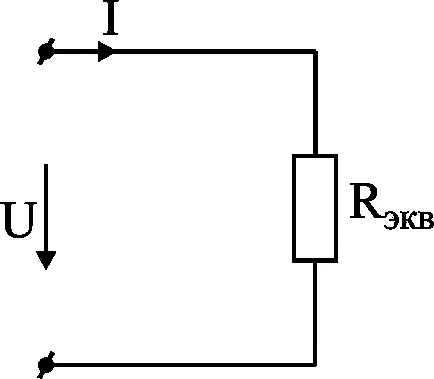
Conversia triunghiului la steaua echivalent.
Conversia într-un triunghi stea echivalent definit a fi un circuit de piesă de schimb conectat la delta, lanț, conectate într-o stea, la care curenții și tensiunile din restul circuitului rămân neschimbate.
Ie o echivalență triunghi și stelele a însemnat că, la aceeași tensiune între aceleași curenții terminale incluse în concluziile același nume sunt aceleași.
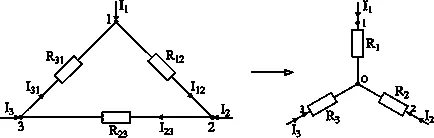
Fig. 3-7. Conversia triunghiului în stea.
Să R12; R23; laturile de rezistență ale triunghiului - R31;
R1; R2; R3 - rezistența stelei;
I12; I23; I31 - curenți în ramurile unui triunghi;
I1; I2; I3 - curenti adecvați la terminalele 1, 2, 3.
Ne exprimăm curenții din ramurile unui triunghi I1 curent adecvat. I2. I3.
Prin lege, suma de tensiune Kirchhoff a căderii de tensiune în triunghiul bucla este egal cu zero:
Conform legii lui Kirchhoff a curenților la nodurile 1 și 2
În rezolvarea acestor ecuații pentru a primi I12:
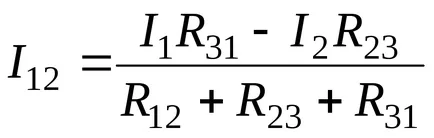
Tensiunea între punctele 1 și 2 din diagrama triunghi:
Tensiunea între aceleași puncte ale schemei stele este:
pentru că este o conversie echivalentă, este necesară egalitatea de tensiuni între punctele de date ale celor două circuite, adică
Acest lucru este posibil în cazul în care:

A treia expresie obținută prin înlocuirea indicilor circulare.
Pe baza expresiei (5) a formulat următoarea regulă:
stele ray Resistance este produsul rezistenței laturilor triunghiului, adiacent grinzii, împărțită la suma rezistenței triunghiului trei laturi.
Conversia stele în triunghi echivalent.
La trecerea de la stea la triunghi sunt cunoscute de rezistență R1. R2. R3 stelei. Valorile rezistenței triunghi este determinat de soluția combinată de ecuații (5):
Partea de rezistență a triunghiului este suma rezistențelor punctelor adiacente ale stelei și lucrările lor, împărțită la rezistența celui de al treilea fascicul.
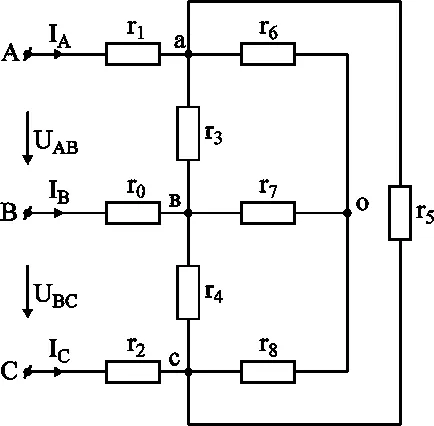
Soluție: Rezistența r6. r7. r8 formează o stea;
rezistență la r3. r4. r5 formează un triunghi.
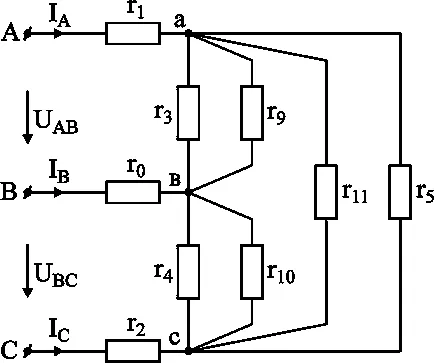
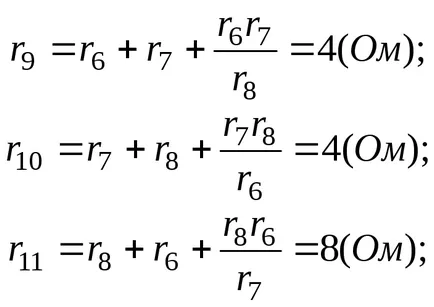
Ca urmare a conversiei au primit două triunghiuri cu laturi paralele (Fig. 3-9). Noi găsim laturile de rezistență echivalente ale triunghiului (Figura 3-10).
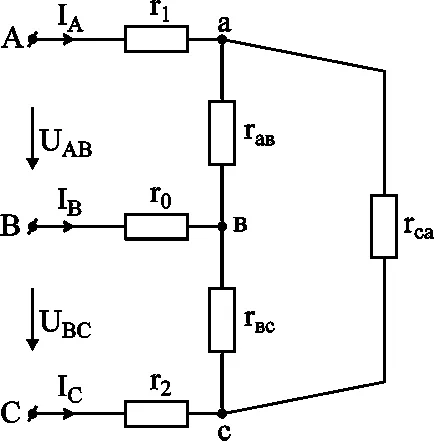
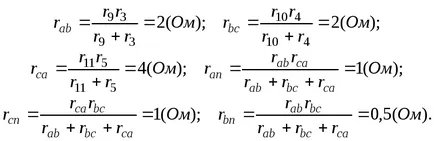
Rezultată transformatei triunghiul stea (Fig. 3-10)
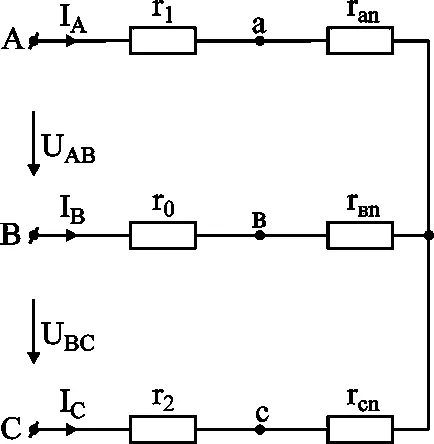
pentru că rezistență la r1; R0; r2 nu sunt supuse transformării, prin care curge curentul IA dorit; BC; IC. Pentru a le găsi, formează un sistem de ecuații de drept lui Kirchhoff:
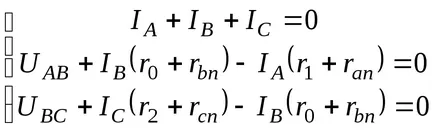
Ca rezultat al soluției obținem:
Conversia unei surse de tensiune cu impedanță internă, o sursă de curent echivalent cu conductivă interior discutat anterior. Necesitatea de a înlocui o specie de o altă sursă de multe ori se produce atunci când rezolvarea problemelor. Trebuie amintit:
Surse echivalente înțeleg curenți invariabilitatea, tensiuni și puteri în circuitul electric extern conectat la sursele.
Conversia activă triunghiul într-o stea activă, și vice-versa, discutate mai jos.
schemele de conversie a circuitelor.
circuite de conversie cu două noduri.
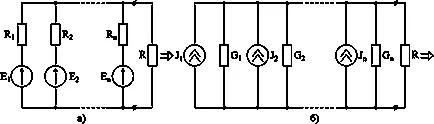
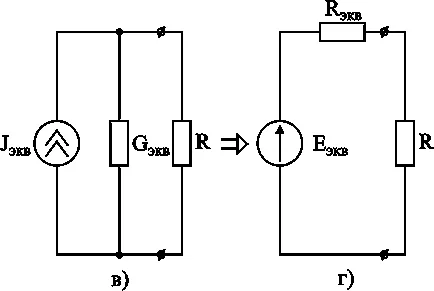
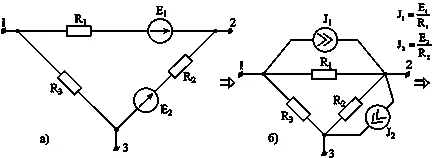
Ris.3-11. Conversia ramurilor de conexiune paralele cu surse de tensiune.
Pe ris.3-11, și diagrama de circuit este prezentat cu două noduri, între care sunt conectate n ramuri paralele cu surse EMF și R. rezistorul Acest sistem este necesar pentru a facilita o singură buclă.
În prima etapă (ris.3-11, b) aplicarea unei reguli a surselor de tensiune și curent echivalente.
Dacă surse de curent n conectate în paralel, sursa de curent echivalent:
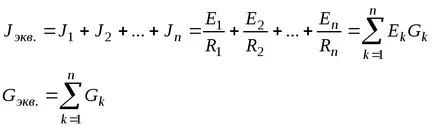
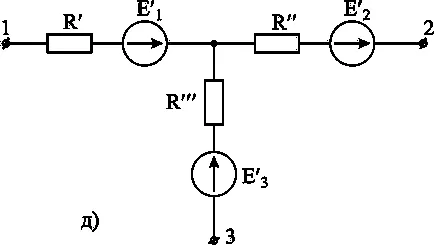
Din diagrama din Fig. 3-11, la rândul său, la schema ris.3-11, r, folosind relațiile:
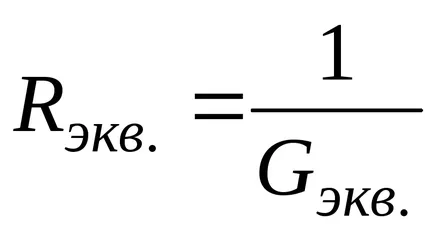
Formula (7) este uneori denumit „formulă pentru un lanț cu două noduri“ sau „Formula două noduri.“
Curentul în circuitul extern (rezistorul R) este egal cu:
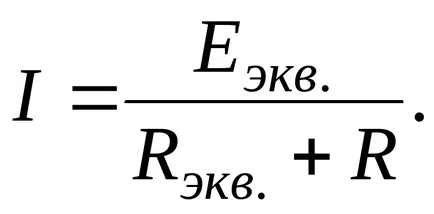
Transferarea surselor în circuit.
Calculul este simplificat, în unele cazuri, circuitul electric ca urmare a surselor de transfer EMF sau curent.
Din ecuațiile lui Kirchhoff se poate observa că curentul în circuit depinde de FME totală în circuitele, nu prin componentele lor individuale. Prin urmare, dacă schimbați poziția surselor EMF de circuit astfel încât FME totală în toate circuitele vor rămâne neschimbate, aceasta nu va afecta curenții de ramură.
În mod similar, tensiunea pe ramuri definite de curentul total al tuturor surselor de energie. Dacă schimbați locația surselor de curent, astfel încât numărul total de curenții din nodurile au rămas neschimbate, aceasta nu va afecta distribuția de stres în circuit.
Condiții de transfer surse de tensiune și surse de curent:
Dacă doriți să excludeți o sursă de tensiune de o ramură, ramura este introdus într-o sursă de tensiune de compensare, și exact aceeași sursă de tensiune este introdusă simultan în toate ramurile, care converg într-un anumit noduri ramură.
Și compensarea sursa de tensiune suplimentară au aceeași direcție în raport cu nodul considerat.
Ca urmare, tensiunea sursei de alimentare a sucursalei sursă este exclusă, și există surse în alte ramuri. Tensiunile combinate în toate circuitele rămân aceleași, respectiv, nu se schimba curenți de ramură.
Concluzie. sursă de tensiune poate fi mutat dintr-un circuit de ramură în toate celelalte ramuri conectate la nodul de ramura, fără a modifica curenții de circuit.
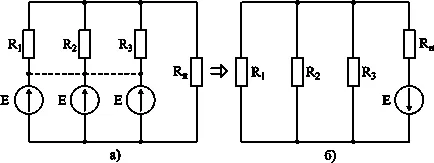
Fig. 3-12. Surse de transfer EMF în circuit.
Deci, în cazul în care în toate ramurile, cu excepția unei reuniuni la nodul au aceeași sursă de tensiune (ris.3-12 la fel de bine), toate direcționate către un singur nod sau un nod, atunci ele pot fi înlocuite cu o singură sursă de tensiune în ramura în în care sursa inițial absentă (ris.3-12 b).
Acest lucru este adevărat, deoarece clipuri de sursă de tensiune pot fi combinate pentru a înțelege egalitatea potențialului lor. Ca urmare a unei astfel de asociere, prezentat în diagrama linie ris.3-12 și punctată se obține ris.3-12 b.
În cazul în care transferul de surse de curent sunt conectate la nodurile de circuit, astfel încât agregatul a rămas constant curenții la nodurile.
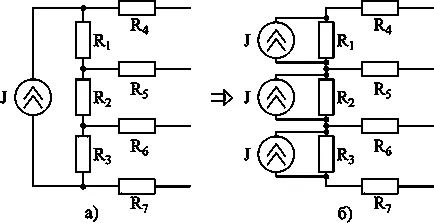
Ris.3-13. Transferul unui circuit sursă de curent.
Pe ris.3-13 și b găzdui o varietate de surse de energie, dar curentul total în ambele circuite sunt aceleași noduri. În consecință, tensiunea dintre noduri nu este schimbat.
Concluzie: Sursa de curent poate fi înlocuită cu o sursă de curent conectată în ramuri paralele, care au fost luate în considerare de circuit cu sursă.
Conversia triunghi activ în stea activă și înapoi.
Transferarea surselor din schema adevărată în practică combinată cu diverse metode de transformare.
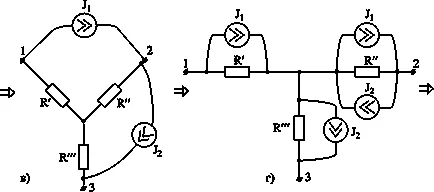
Următoarele scheme demonstrează procedura dată de transformare triunghi activ la steaua activă.
Sub triunghiul activ se referă la ramurile de circuit sunt conectate în triunghi și conțin în plus față de rezistoare surse de emf
O stea activă se referă la conexiunea de sucursale într-o stea a cărei raze conțin rezistențe și surse de emf
Fig. 4a prezintă surse o parte a circuitului conectat în triunghi, ramurile cărora sunt incluse emf