0 Cercul de Apolonius

0.6. Apollonios cerc

Luați în considerare problema de a găsi locul geometric al punctelor în plan, raportul dintre distanțele de la care la cele două puncte de date - constanta. Pentru a rezolva această problemă folosim metoda de coordonate, și anume obținem formele de ecuații formate de locus și apoi studiați proprietățile geometrice.

Introducem un sistem de coordonate rectangulare, selectarea ca punct de pornire unul din cele două puncte date A și B (de exemplu, B), iar axa Ox - astfel încât al doilea punct (Să-ți fie punctul A), situată pe o jumătate pozitivă (a se vedea figura 10.6 .. .1).

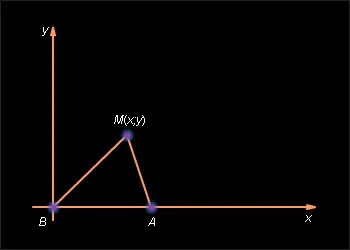
In acest sistem de coordonate, punctul B are coordonatele (0, 0), iar punctul A - (a, 0), unde a> 0. Fie M (. X y) - un punct arbitrar ce satisface condiția problemei, adică AM = k · BM. unde k - având în vedere numărul pozitiv. Dacă k = 1, aceasta înseamnă că setul dorit constă din puncte echidistante față de punctele de date A și B. Proprietățile perpendicular pe segmentul, rezultă că setul dorit în acest caz, este o linie dreaptă care trece prin mijlocul perpendiculara a segmentului AB axa OX. Acum, să k ≠ 1. Din Teorema 10.2 avem și starea punctului M consumabile setul dorit poate fi scris ca

Această ecuație este echivalentă cu egalitati

Singularizarea un pătrat perfect, vom obține

Această ecuație a unui cerc cu centrul în punctul situată pe axa OX. și raza

Cercul rezultat este numit după geometru grec antic Apollonios. a decis să însărcineze o metodă pur geometrică.
pagina 1

0 Cercul de Apolonius
16.36kb. 1 p.

Ellipse Tool și mențineți apăsată tasta Ctrl, trage două cercuri, unul dintre care un diametru puțin mai mare decât acesta din urmă. cerc mai mic este completat utilizând instrumentul Fointain Fill
15.18kb. 1 p.